《2025年5年中考3年模拟九年级数学全一册苏科版》

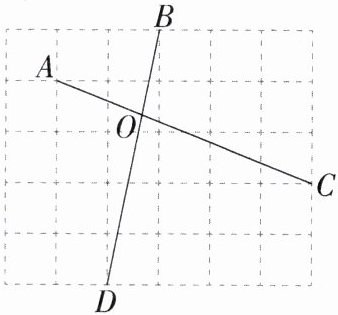
5.「2024江苏南通如皋期末」如图,在边长为1的小正方形组成的网格中,点A,B,C,D在小正方形的顶点处,AC与BD相交于点O,则AO的长为( )


A.$\frac{\sqrt{29}}{3}$
B.$\frac{\sqrt{26}}{3}$
C.$\frac{\sqrt{29}}{2}$
D.$\frac{\sqrt{26}}{2}$

答案：
A　如图，AG=2，BG=1，DH=2，CH=4，
∴$\frac{AG}{GB}=\frac{CH}{DH}=2$，AB=$\sqrt{AG^2+BG^2}=\sqrt{5}$，CD=$\sqrt{DH^2+CH^2}=\sqrt{20}=2\sqrt{5}$，
∴$\frac{AG}{CH}=\frac{GB}{DH}$，
∵∠AGB=∠CHD=90°，
∴△AGB∽△CHD，
∴∠BAG=∠DCH。
∵AG//CH，
∴∠GAC=∠HCA，
∴∠BAO=∠DCO。
∵∠AOB=∠COD，
∴△AOB∽△COD，
∴$\frac{AO}{OC}=\frac{AB}{CD}=\frac{1}{2}$，
∴AO=$\frac{1}{2}$OC，
∴AO=$\frac{1}{3}$AC。
∵AC=$\sqrt{2^2+5^2}=\sqrt{29}$，
∴AO=$\frac{\sqrt{29}}{3}$。故选A。

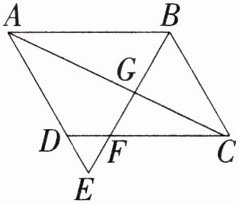
6.「2025无锡天一中学月考」如图,在平行四边形ABCD中,E是边AD的延长线上一点,连接BE交CD于点F,交对角线AC于点G。
(1)若DE= 1,AD= 2,求$\frac{CF}{DF}$的值。
(2)求证：△BCF∽△EAB。

答案： 解析　
(1)
∵四边形ABCD是平行四边形，
∴BC//AE，BC=AD=2，
∴△CBF∽△DEF，
∴$\frac{CF}{DF}=\frac{BC}{DE}=\frac{2}{1}=2$。
(2)证明：
∵四边形ABCD是平行四边形，
∴BC//AE，∠BAE=∠FCB，
∴∠E=∠CBF，
∴△BCF∽△EAB。

7.「2024江苏南京鼓楼期末」如图,将等边三角形纸片ABC折叠,使点A落在边BC上的点D处,MN为折痕。若$\frac{BD}{DC}= \frac{1}{2}$,则$\frac{AM}{AN}$的值为(C)
A.$\frac{1}{2}$
B.$\frac{2}{3}$
C.$\frac{4}{5}$
D.$\frac{5}{7}$

答案： C
∵△ABC是等边三角形，
∴∠A=∠B=∠C=60°，由折叠可知，AM=DM，AN=DN，∠A=∠MDN=60°，
∴∠BDM+∠CDN=120°，
∵∠BDM+∠BMD=120°，
∴∠BMD=∠CDN，
∵∠B=∠C，
∴△BDM∽△CND，
∴$\frac{BD}{CN}=\frac{BM}{CD}=\frac{DM}{ND}$，
∵$\frac{BD}{DC}=\frac{1}{2}$，
∴设BD=x，则CD=2x，
∴BC=AB=AC=3x，设AM=DM=k，
∴BM=3x−k，
∴$\frac{x}{CN}=\frac{3x-k}{2x}=\frac{k}{DN}$，
∴CN=$\frac{2x^2}{3x-k}$，DN=$\frac{2xk}{3x-k}$，
∵DN+CN=AN+CN=AC=3x，
∴$\frac{2x^2}{3x-k}+\frac{2xk}{3x-k}=3x$，
∴k=$\frac{7}{5}x$，
∴DN=$\frac{2x\cdot\frac{7}{5}x}{3x-\frac{7}{5}x}=\frac{7}{4}x$，
∴$\frac{AM}{AN}=\frac{DM}{DN}=\frac{\frac{7}{5}x}{\frac{7}{4}x}=\frac{4}{5}$，故选C。

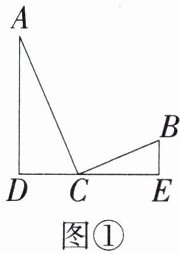
8.(1)如图①,已知∠ADC= ∠BEC= ∠ACB= 90°,D、C、E三点共线,求证：△ADC∽△CEB。
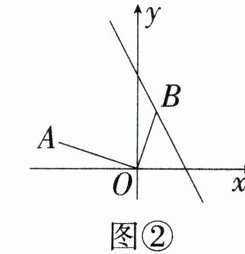
(2)如图②,已知点A(-3,1),点B在直线y= -2x+4上,若∠AOB= 90°,求点B的坐标。

答案：
解析　
(1)证明：
∵∠ADC=∠BEC=∠ACB=90°，
∴∠A+∠ACD=∠ACD+∠BCE=90°，
∴∠A=∠BCE，
∴△ADC∽△CEB。
(2)如图，过点A作AC⊥x轴于点C，过点B作BE⊥x轴于点E，
∵A(−3,1)，
∴AC=1，OC=3，
∵∠AOB=90°，
∴∠A+∠AOC=∠AOC+∠BOE=90°，
∴∠A=∠BOE，
∵∠ACO=∠OEB=90°，
∴△ACO∽△OEB，
∴$\frac{AC}{OE}=\frac{OC}{BE}$，
∵点B在直线y=−2x+4上，
∴设B(a,−2a+4)，则$\frac{1}{a}=\frac{3}{-2a+4}$，解得a=$\frac{4}{5}$，
∴点B的坐标为$(\frac{4}{5},\frac{12}{5})$。