《2025年5年中考3年模拟九年级数学全一册苏科版》

1. 已知 $\sin A = 0.8192$,运用科学计算器求锐角 $A$ 时(在开机状态下),按下的第一个键是(D)

答案： 1.D　求多少度角的正弦值是0.8192,需要先按2ndF 键,接着按sin键,再输入数值.故选D.

2. 「2024 山东淄博淄川期末」如图,为方便行人推车过天桥,某市政府在 $10\ \text{m}$ 高的天桥两端分别修建了 $40\ \text{m}$ 长的斜道,用科学计算器计算其中一条斜道的倾斜角 $\angle A$,下列按键顺序正确的是(A)

答案： 2.A　sinA=$\frac{BC}{AC}$=$\frac{10}{40}$=0.25,故选A.

3. 求满足下列等式的锐角 $\theta$ 的度数(非特殊角精确到 $0.1^{\circ}$,可借助计算器)：
(1)$\tan(\theta - 15^{\circ}) = 2.4378$。
(2)$2\cos^2\theta - 5\cos\theta + 2 = 0$。

答案： 3.解析　
(1)
∵tan(θ - 15°) = 2.4378,
∴θ - 15°≈67.7°,
∴θ = 82.7°.
(2)
∵2cos²θ - 5cosθ + 2 = 0,
∴(2cosθ - 1)(cosθ - 2) = 0,
∴cosθ = $\frac{1}{2}$或cosθ = 2,
∵θ为锐角,
∴cosθ = $\frac{1}{2}$,
∴θ = 60°.

4. 学 教材变式 特色 P108 习题 T2
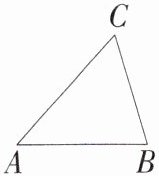
如图,在 $\triangle ABC$ 中,$AB = 8$,$AC = 9$,$\angle A = 48^{\circ}$。
(1)求 $AB$ 边上的高(结果精确到 $0.01$)。
(2)求 $\angle B$ 的度数(结果精确到 $1'$)。

答案：
4.解析　
(1)作AB边上的高CH,垂足为H,
　　　　　　　　　
∵在Rt△ACH中,sinA=$\frac{CH}{AC}$,
∴CH=AC·sinA=9sin48°≈6.69.
(2)
∵在Rt△ACH中,cosA=$\frac{AH}{AC}$,
∴AH=AC·cosA=9cos48°,
∴在Rt△BCH中,tanB=$\frac{CH}{BH}$=$\frac{CH}{AB−AH}$=$\frac{9sin48°}{8−9cos48°}$≈3.382,
∴∠B≈73°32'.

5. 「2023 山东济南莱芜期末,★☆」如图,要想使人安全攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角 $\alpha$ 一般要满足 $60^{\circ} \leq \alpha \leq 75^{\circ}$,现有一架长 $10$ 米的梯子。(参考数据：$\sin 75^{\circ} \approx 0.97$,$\cos 75^{\circ} \approx 0.26$,$\tan 75^{\circ} \approx 3.73$,$\sin 23.6^{\circ} \approx 0.40$,$\cos 66.4^{\circ} \approx 0.40$,$\tan 21.8^{\circ} \approx 0.40$)
(1)使用这架梯子最高可以安全攀上多高的墙？
(2)当梯子底端距离墙面 $4$ 米时,$\alpha$ 等于多少度？此时人是否能够安全使用这架梯子？

答案： 5.解析　
(1)在Rt△ABC中,∠ACB=90°,AB=10米,
∴AC=AB·sin∠ABC=10sinα米,
∵60°≤α≤75°,
∴当α=75°时,AC最大=10sin75°≈9.7(米),
∴使用这架梯子最高可以安全攀上9.7米的墙.
(2)在Rt△ABC中,∠ACB=90°,AB=10米,BC=4米,
∴cos∠ABC=$\frac{BC}{AB}$=$\frac{2}{5}$,
∴α≈66.4°,
∵60°＜66.4°＜75°,
∴此时人能够安全使用这架梯子.

6. 「2024 江苏扬州中考,★☆」如图 1,将两个宽度相等的矩形纸条叠放在一起,得到四边形 $ABCD$。
(1)试判断四边形 $ABCD$ 的形状,并说明理由。
(2)已知矩形纸条的宽度为 $2\ \text{cm}$,将矩形纸条旋转至如图 2 所示的位置时,四边形 $ABCD$ 的面积为 $8\ \text{cm}^2$,求此时直线 $AD$、$CD$ 所夹锐角 $\angle 1$ 的度数。

答案：
6.解析　
(1)四边形ABCD是菱形.理由如下:
　如图1,过C作CH⊥AB于H,CG⊥AD于G,
∵两个纸条为矩形,
∴AB//CD,AD//BC,
∴四边形ABCD是平行四边形，
∵SABCD=AB·CH=AD·CG,且CH=CG,
∴AB=AD,
∴四边形ABCD是菱形.
　　　　　
(2)如图2,过A作AM⊥CD于M,
∵S菱形ABCD=CD·AM=8cm²,且AM=2cm,
∴CD=4cm,
∴AD=CD=4cm,
　在Rt△ADM中,sin∠1=$\frac{AM}{AD}$=$\frac{1}{2}$,
∴∠1=30°.