《2025年5年中考3年模拟九年级数学全一册苏科版》

12.「2024西藏中考」甲、乙、丙三名学生参加仰卧起坐体育项目测试,他们一周测试成绩的平均数相同,方差如下:$s^{2}_{甲}= 1.5,s^{2}_{乙}= 3.4,s^{2}_{丙}= 0.9$,则甲、乙、丙中成绩最稳定的学生是丙.

答案： 丙 解析
∵甲、乙、丙三名学生的平均数相同，$s^{2}_{\text{甲}} = 1.5$，$s^{2}_{\text{乙}} = 3.4$，$s^{2}_{\text{丙}} = 0.9$，
∴$s^{2}_{\text{丙}} ＜ s^{2}_{\text{甲}} ＜ s^{2}_{\text{乙}}$，
∴甲、乙、丙中成绩最稳定的是丙。

13.点P是$\odot O$外一点,PA、PB分别与$\odot O$相切于A、B两点,$∠APB= 60^{\circ }$,点C为$\odot O$上一点(点C不与A、B重合),连接AC、BC,则$∠ACB= $$60^{\circ}$或$120^{\circ}$.

答案： $60^{\circ}$或$120^{\circ}$ 解析 如图，连接OA，OB。
∵PA、PB分别与$\odot O$相切于A、B两点，
∴$\angle OAP = \angle OBP = 90^{\circ}$，
∵$\angle APB = 60^{\circ}$，$\angle AOB + \angle OAP + \angle OBP + \angle APB = 360^{\circ}$，
∴$\angle AOB = 120^{\circ}$，当点C在优弧AB上时，$\angle ACB = \frac{1}{2}\angle AOB = 60^{\circ}$；当点C在劣弧AB上时，$\angle AC'B = 180^{\circ} - 60^{\circ} = 120^{\circ}$。综上，$\angle ACB = 60^{\circ}$或$120^{\circ}$。

14.「2023江苏南京南师附中新城分校二模」若一组数据1,3,5,a,8的方差是2,则另一组数据3,9,15,3a,24的方差是18.

答案： 18 解析
∵一组数据1,3,5,a,8的方差是2，
∴另一组数据3,9,15,3a,24的方差是$2×3^2 = 18$。

15.「2024山东青岛中考」如图,某小区要在长为16 m,宽为12 m的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为空地面积的一半,则小路的宽为2m.

答案： 2 解析 设小路的宽为x m，根据题意得$(16 - 2x)(12 - 2x) = \frac{1}{2}×12×16$，解得$x = 2$或$x = 12$（舍去），
∴小路的宽为2m。

16.「2024山东德州中考」已知a和b是方程$x^{2}+2024x-4= 0$的两个解,则$a^{2}+2023a-b$的值为2028.

答案： 2028 解析
∵a和b是方程$x^2 + 2024x - 4 = 0$的两个解，
∴$a^2 + 2024a - 4 = 0$①，$a + b = -2024$②，① - ②得，$a^2 + 2024a - 4 - a - b = 2024$，
∴$a^2 + 2023a - 4 - b = 2024$，
∴$a^2 + 2023a - b = 2028$。

17.「2023四川广元中考」如图,$∠ACB= 45^{\circ }$,半径为2的$\odot O$与角的两边相切,点P是$\odot O$上任意一点,过点P向角的两边作垂线,垂足分别为E、F,设$t= PE+\sqrt {2}PF$,则t的取值范围是____$2\sqrt{2}\leqslant t\leqslant4 + 2\sqrt{2}$.

答案： $2\sqrt{2}\leqslant t\leqslant4 + 2\sqrt{2}$ 解析 设半径为2的$\odot O$与角的两边分别相切于点M、点N，连接OM、ON，延长NO交CB于点D，
∴$\angle CND = \angle OMD = 90^{\circ}$，
∵$\angle ACB = 45^{\circ}$，
∴$\angle NDC = 45^{\circ}$，
∴$\triangle CND$与$\triangle OMD$都是等腰直角三角形，
∵$ON = OM = 2$，
∴$OD = 2\sqrt{2}$，
∴$CN = DN = 2 + 2\sqrt{2}$，如图1，延长EP交BC于点Q，
∵$EQ\perp AC$，$PF\perp BC$，
∴$\angle CEQ = \angle PFQ = 90^{\circ}$，
∵$\angle ACB = 45^{\circ}$，
∴$\angle EQC = 45^{\circ}$，
∴$\triangle ECQ$与$\triangle PFQ$都是等腰直角三角形，
∴$CE = EQ$，$PQ = \sqrt{2}PF$，
∴$t = PE + \sqrt{2}PF = PE + PQ = EQ$，当EQ与$\odot O$相切且点P在圆心的右侧时，t有最大值，连接OP，则四边形ENOP是正方形，
∴$EN = OP = 2$，
∴$t = PE + \sqrt{2}PF = EQ = CE = CN + EN = 2 + 2\sqrt{2} + 2 = 4 + 2\sqrt{2}$；如图2，当EQ与$\odot O$相切且点P在圆心的左侧时，t有最小值，同理可得$t = PE + \sqrt{2}PF = PE + PQ = EQ = CE = CN - EN = 2 + 2\sqrt{2} - 2 = 2\sqrt{2}$。故t的取值范围是$2\sqrt{2}\leqslant t\leqslant4 + 2\sqrt{2}$。

18.如图,以$G(0,2)$为圆心,4为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为$\odot G$上一动点,$CF⊥AE$于点F,则线段FG的长度的最小值为____.

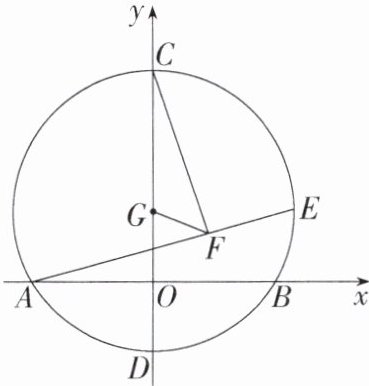
$2\sqrt{3} - 2$

答案： $2\sqrt{3} - 2$ 解析 连接AC，过点G作$GM\perp AC$于点M，连接AG，如图所示。
∵$GO\perp AB$，$G(0,2)$，
∴$OG = 2$，$\angle AOG = 90^{\circ}$，在$Rt\triangle AGO$中，
∵$AG = 4$，
∴$AG = 2OG$，$OA = \sqrt{4^2 - 2^2} = 2\sqrt{3}$，
∴$\angle GAO = 30^{\circ}$，
∴$\angle AGO = 60^{\circ}$，
∵$GC = GA = 4$，
∴$\angle GCA = \angle GAC$，$AM = CM$，
∵$\angle AGO = \angle GCA + \angle GAC$，
∴$\angle GCA = \angle GAC = 30^{\circ}$，
∴$AC = 2OA = 4\sqrt{3}$，$MG = \frac{1}{2}GC = 2$，
∵$CF\perp AE$，
∴$\angle AFC = 90^{\circ}$，
∴点F在以AC为直径的$\odot M$上，当点F在MG的延长线上时，FG的长度最小，最小值=$FM - MG = \frac{1}{2}AC - MG = 2\sqrt{3} - 2$。

19.「2025江苏常州外国语学校月考」(8分)解下列方程:
(1)$x^{2}-4x-3= 0$.
(2)$x(x-4)-(2x-8)= 0$.

答案： 解析
(1)移项，得$x^2 - 4x = 3$，配方，得$x^2 - 4x + 4 = 3 + 4$， (1分)即$(x - 2)^2 = 7$， (2分)
∴$x - 2 = \pm\sqrt{7}$， (3分)
∴$x_1 = 2 + \sqrt{7}$，$x_2 = 2 - \sqrt{7}$。 (4分)
(2)
∵$x(x - 4) - (2x - 8) = 0$
∴$x(x - 4) - 2(x - 4) = 0$， (5分)
∴$(x - 4)(x - 2) = 0$， (6分)
∴$x - 4 = 0$或$x - 2 = 0$， (7分)
∴$x_1 = 4$，$x_2 = 2$。 (8分)

20.「2024江苏徐州中考」(6分)不透明的袋子中装有2个红球与2个白球,这些球除颜色外无其他差别.
(1)甲从袋子中随机摸出1个球,摸到红球的概率为0.5.
(2)甲、乙两人分别从袋子中随机摸出1个球(不放回),用列表或画树状图的方法,求两人摸到相同颜色球的概率.
画树状图如图：由树状图可得共有12种等可能的结果，其中甲、乙两人摸到相同颜色球的结果有4种，∴P(甲、乙两人摸到相同颜色球)=$\frac{4}{12} = \frac{1}{3}$。

答案： 解析
(1)0.5。 (2分)
(2)画树状图如图：由树状图可得共有12种等可能的结果，其中甲、乙两人摸到相同颜色球的结果有4种， (5分)
∴P(甲、乙两人摸到相同颜色球)=$\frac{4}{12} = \frac{1}{3}$。 (6分)