《2025年5年中考3年模拟九年级数学全一册苏科版》

10. 「2025江苏苏州水平调研」对于一个函数,当自变量x取n时,函数值y等于3n,我们称n为这个函数的“三倍数”.若二次函数$y= x^{2}+7x+2c$有且只有一个“三倍数”,则c的值为2.

答案： 2 解析　由题意，得方程$3n=n^{2}+7n+2c$有且只有一个实数解，即$n^{2}+4n+2c=0$有且只有一个实数解，故$4^{2}-4×1×2c=0$，解得$c=2$。

11. 「2024广西中考」如图,壮壮同学投掷实心球,出手(点P处)的高度OP是$\frac {7}{4}m$,出手后实心球沿一段抛物线运行,到达最高点时,水平距离是5m,高度是4m.若实心球落地点为M,则$OM=$$\frac{35}{3}$m.

答案： $\frac{35}{3}$解析　以点O为坐标原点，直线OM为x轴，直线OP为y轴，建立平面直角坐标系，设抛物线解析式为$y=a(x-5)^{2}+4$，把$(0,\frac{7}{4})$代入得$25a+4=\frac{7}{4}$，解得$a=-\frac{9}{100}$，$\therefore$抛物线解析式为$y=-\frac{9}{100}(x-5)^{2}+4$。$\because$M为抛物线与x轴的交点，令$y=-\frac{9}{100}(x-5)^{2}+4=0$，解得$x_{1}=\frac{35}{3}$，$x_{2}=-\frac{5}{3}$（不合题意，舍去），$\therefore OM=\frac{35}{3}m$。

12. 「2025江苏苏州工业园区星海中学期中」(10分)已知二次函数$y= -x^{2}-(m-1)x+m+1$.
(1)求证:无论m取何值,该函数图像与x轴总有两个交点.
(2)若该函数图像的对称轴是直线$x= 1$,将该函数的图像向下平移h个单位长度与x轴只有一个交点,求h的值.

答案： 解析　
(1)证明：$\because$二次函数为$y=-x^{2}-(m-1)x+m+1$，$\therefore b^{2}-4ac=(m-1)^{2}+4(m+1)=m^{2}-2m+1+4m+4=m^{2}+2m+5=(m+1)^{2}+4\geqslant4＞0$，$\therefore$无论m取何值，该函数图像与x轴总有两个交点。
(2)$\because$二次函数为$y=-x^{2}-(m-1)x+m+1$，$\therefore$图像的对称轴是直线$x=1$，$\therefore -\frac{-(m-1)}{2×(-1)}=1$，$\therefore m=-1$，$\therefore$二次函数为$y=-x^{2}+2x=-(x-1)^{2}+1$。将函数$y=-(x-1)^{2}+1$的图像向下平移h个单位长度后图像对应的解析式为$y=-(x-1)^{2}+1-h$，由题意得$1-h=0$，$\therefore h=1$。

13. 「2024贵州中考」(14分)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
|销售单价x/元|…|12|14|16|18|20|…|
|销售量y/盒|…|56|52|48|44|40|…|
(1)求y与x的函数表达式.
(2)糖果销售单价定为多少元时,所获日销售利润最大?最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.

答案： 解析　
(1)设y与x的函数表达式为$y=kx+b$，把$x=12$，$y=56$；$x=20$，$y=40$代入，得$\left\{\begin{array}{l}12k+b=56\\20k+b=40\end{array}\right.$，解得$\left\{\begin{array}{l}k=-2\\b=80\end{array}\right.$，$\therefore$y与x的函数表达式为$y=-2x+80$。
(2)设日销售利润为w元，根据题意，得$w=(x-10)\cdot y=(x-10)(-2x+80)=-2x^{2}+100x-800=-2(x-25)^{2}+450$，$\therefore$当$x=25$时，w取得最大值，为450，$\therefore$糖果销售单价定为25元时，所获日销售利润最大，最大利润是450元。
(3)设日销售利润为w元，根据题意，得$w=(x-10-m)\cdot y=(x-10-m)(-2x+80)=-2x^{2}+(100+2m)x-800-80m$，$\therefore$当$x=-\frac{100+2m}{2×(-2)}=\frac{50+m}{2}$时，w有最大值，为$-2(\frac{50+m}{2})^{2}+(100+2m)(\frac{50+m}{2})-800-80m$。$\because$糖果日销售获得的最大利润为392元，$\therefore -2(\frac{50+m}{2})^{2}+(100+2m)(\frac{50+m}{2})-800-80m=392$，化简得$m^{2}-60m+116=0$，解得$m_{1}=2$，$m_{2}=58$。当$m=58$时，$x=\frac{50+58}{2}=54$，此时每盒的利润为$(54-10-58)$元$＜0$元，故舍去，$\therefore m$的值为2。

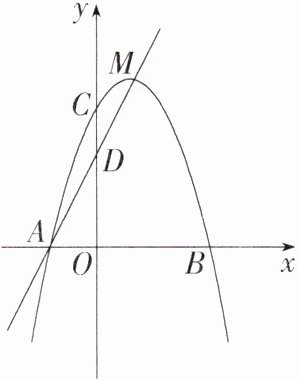
14. 「2023山东枣庄中考」(14分)如图,抛物线$y= -x^{2}+bx+c经过A(-1,0)$,$C(0,3)$两点,并交x轴于另一点B,点M是抛物线的顶点,直线AM与y轴交于点D.
(1)求该抛物线的表达式.
(2)若点H是x轴上一动点,分别连接MH,DH,求$MH+DH$的最小值.
(3)若点P是抛物线上一动点,问在对称轴上是否存在点Q,使得以D,M,P,Q为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.

答案： 解析　
(1)$\because$抛物线$y=-x^{2}+bx+c$经过$A(-1,0)$，$C(0,3)$两点，$\therefore \left\{\begin{array}{l}-1-b+c=0\\c=3\end{array}\right.$，解得$\left\{\begin{array}{l}b=2\\c=3\end{array}\right.$，$\therefore$该抛物线的表达式为$y=-x^{2}+2x+3$。
(2)$\because y=-x^{2}+2x+3=-(x-1)^{2}+4$，$\therefore$顶点M的坐标为$(1,4)$，设直线AM的解析式为$y=kx+d(k\neq0)$，则$\left\{\begin{array}{l}k+d=4\\-k+d=0\end{array}\right.$，解得$\left\{\begin{array}{l}k=2\\d=2\end{array}\right.$，$\therefore$直线AM的解析式为$y=2x+2$，当$x=0$时，$y=2$，$\therefore D(0,2)$，作点D关于x轴的对称点$D'(0,-2)$，连接$D'M$，$D'H$，如图，则$DH=D'H$，$\therefore MH+DH=MH+D'H\geqslant D'M$，即$MH+DH$的最小值为$D'M$的长，$\because D'M=\sqrt{(1-0)^{2}+(4+2)^{2}}=\sqrt{37}$，$\therefore MH+DH$的最小值为$\sqrt{37}$。
(3)对称轴上存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形。点Q的坐标为$(1,3)$或$(1,1)$或$(1,5)$。详解：由
(2)得，$D(0,2)$，$M(1,4)$，$\because$点P是抛物线上一动点，$\therefore$可设$P(m,-m^{2}+2m+3)$，$\because$抛物线$y=-x^{2}+2x+3$的对称轴为直线$x=1$，$\therefore$可设$Q(1,n)$。①当DM、PQ为对角线时，DM、PQ的中点重合，$\therefore \left\{\begin{array}{l}0+1=m+1\\2+4=-m^{2}+2m+3+n\end{array}\right.$，解得$\left\{\begin{array}{l}m=0\\n=3\end{array}\right.$，$\therefore Q(1,3)$；②当DP、MQ为对角线时，DP、MQ的中点重合，$\therefore \left\{\begin{array}{l}0+m=1+1\\2-m^{2}+2m+3=4+n\end{array}\right.$，解得$\left\{\begin{array}{l}m=2\\n=1\end{array}\right.$，$\therefore Q(1,1)$；③当DQ、PM为对角线时，DQ、PM的中点重合，$\therefore \left\{\begin{array}{l}0+1=1+m\\2+n=4-m^{2}+2m+3\end{array}\right.$，解得$\left\{\begin{array}{l}m=0\\n=5\end{array}\right.$，$\therefore Q(1,5)$。综上所述，对称轴上存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形，点Q的坐标为$(1,3)$或$(1,1)$或$(1,5)$。