《2025年5年中考3年模拟九年级数学全一册苏科版》

1. 下列结论中,错误的有(B)
①弦的垂直平分线经过圆心；②平分弦的直径垂直于弦；③平分弧的直径垂直平分这条弧所对的弦；④平分弦的直径,平分这条弦所对的弧。
A.1 个
B.2 个
C.3 个
D.4 个

答案： 1.B　平分弦(不是直径)的直径垂直于弦，平分弦(不是直径)的直径，平分这条弦所对的弧，故②④错误，易知①③正确.故选B.

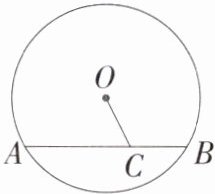
2. 「2025 江苏徐州邳州期中」如图,在半径为 5 的$\odot O$中,弦$AB = 8$,点$C是弦AB$上的一动点,若$OC$的长为整数,则满足条件的点$C$有( )


A.3 个
B.4 个
C.5 个
D.6 个

答案：
2.C　如图所示,过点O作OD⊥AB于D,连接OA,

∴AD=$\frac{1}{2}$AB=4,在Rt△AOD中,由勾股定理得OD=$\sqrt{OA^2 - AD^2}=\sqrt{5^2 - 4^2}=3$,
∵C是弦AB上的一动点,
∴OD≤OC≤OA,即3≤OC≤5,
∵OC 的长为整数,
∴OC的长为3,4,5.当OC=3时,有一个点满足题意;当OC=4时,有两个点满足题意;当OC=5时,两个点满足题意
∴一共有5个点满足题意.故选C.

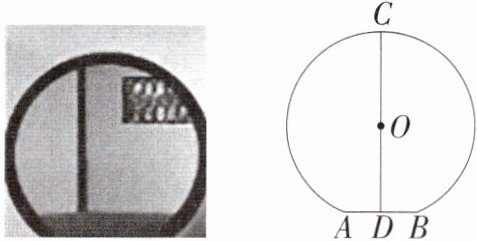
3. 「2024 内蒙古通辽中考」如图,圆形拱门最下端$AB$在地面上,$D为AB$的中点,$C$为拱门最高点,线段$CD$经过拱门所在圆的圆心,若$AB = 1m$,$CD = 2.5m$,则拱门所在圆的半径为( )


A.1.25 m
B.1.3 m
C.1.4 m
D.1.45 m

答案：
3.B　如图,连接OA.

∵D为AB的中点,C为拱门最高点线段CD经过拱门所在圆的圆心,AB=1m,
∴CD⊥AB,AD=BD=05m设拱门所在圆的半径为r m则OA=OC=r m,
∵CD=25m,
∴OD=(25 - r)m,在Rt△AOD中,由勾股定理得$r^2 = 0.5^2 + (2.5 - r)^2$,解得r=13,
∴拱门所在圆的半径为1.3m.故选B.

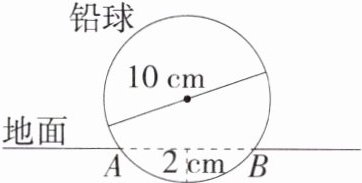
4. 「2025 江苏宿迁宿城期中」在练习掷铅球项目时,某同学掷出的铅球直径为 10 cm,在操场地上砸出一个深 2 cm 的小坑,如图,则该坑的直径$AB$为______cm。

答案：
4.答案　8
解析　如图,过点O作OE⊥AB于点D,交圆O于点E,连接OA,

根据题意得DE=2cm,OA=OE=$\frac{1}{2}×10 = 5$(cm),
∴OD=5 - 2=3(cm),
∴在Rt△AOD中,AD=$\sqrt{OA^2 - OD^2}=4$cm,
∵OE⊥AB,
∴AB=2AD=8cm.

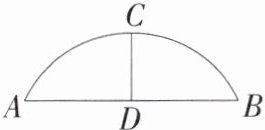
5. 新考向 数学文化「2025 江苏南通海安期中,」“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题：“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯长一尺,问径如何？”问题翻译：如图,现有圆形木材埋在墙壁里,不知木材大小,将它锯下来测得深度$CD$为 1 寸,锯长$AB$为 10 寸,则圆形木材的半径为______寸。

答案：
5.答案　13
解析　设圆形木材的圆心为O,延长CD交⊙O于点E,连接OA,如图所示.

由题意知,CE过点O,且OC⊥AB,则AD=BD=$\frac{1}{2}$AB=5寸,设圆形木材的半径为r寸,则OD=(r - 1)寸,OA=r寸,在Rt△AOD中,
∵$OA^2 = OD^2 + AD^2$,
∴$r^2=(r - 1)^2 + 5^2$,解得r=13,
∴圆形木材的半径为13寸.

6. 「2025 江苏泰州姜堰期中,」如图,在$\odot O$中,$\overset{\frown}{AB}= 2\overset{\frown}{BC}$,且$BD\perp OC$,垂足为$D$。若$AB = 8$,$CD = 2$,则$\odot O$的半径为______。

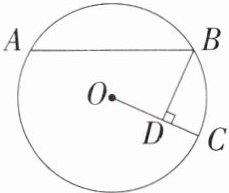
答案：
6.答案　5
解析　如图,过点O作AB的垂线交AB于点E,交$\overset{\frown}{AB}$于点F,连接OB.

∵OF⊥AB,AB=8,
∴$\overset{\frown}{AF}=\overset{\frown}{BF}=\frac{1}{2}\overset{\frown}{AB}$,AE=BE=$\frac{1}{2}$AB=$\frac{1}{2}×8 = 4$,
∵$\overset{\frown}{AB}=2\overset{\frown}{BC}$,
∴$\overset{\frown}{BC}=\overset{\frown}{BF}$,
∴∠BOC=∠BOF,
∵BD⊥OC,OF⊥AB,
∴BD=BE=4,设⊙O的半径为r,则OB=OC=r,
∵CD=2,
∴OD=OC - CD=r - 2,在Rt△BOD中,利用勾股定理,得$BD^2 + OD^2 = OB^2$,
∴$4^2 + (r - 2)^2 = r^2$,
∴r=5,
∴⊙O的半径为5.

7. 「2024 江苏南师附中树人学校月考,」如图,点$C是AE$的中点,在$AE同侧分别以AC$、$CE为直径作半圆B$、半圆$D$。直线$l// AE$,且与两个半圆依次相交于$F$、$M$、$N$、$G$不同的四点。若$AE = 10$,$FG = x$,$MN = y$,则$y与x$之间的函数表达式为______。

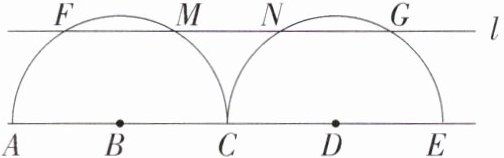
答案：
7.答案　y = 10 - x
解析　过B点作BQ⊥FM于Q,过D点作DH⊥NG于H,连接BF、DG,如图,

则FQ=MQ,NH=GH,
∵l//AE,
∴BQ=DH,BQ⊥AE,DH⊥AE,
∴四边形BDHQ为矩形,
∴QH=BD=$\frac{1}{2}$AE=5,
∴QM + MN + NH=5,
∴QM + NH=5 - y,
∵FQ=$\sqrt{BF^2 - BQ^2}$,GH=$\sqrt{DG^2 - DH^2}$,BF=DG,
∴FQ=GH,
∴FQ=MQ=NH=GH,
∵FG=FM + MN + NG=2QM + MN + 2NH=2(QM + NH) + MN,
∴x=2(5 - y) + y=10 - y,
∴y=10 - x.

8. 新课标 几何直观「2024 江苏宿迁宿豫期中」如图,在平面直角坐标系$xOy$中,以原点$O为圆心的圆过点A(13,0)$,直线$y = kx - 3k + 4(k\neq0)与\odot O交于B$、$C$两点,则弦$BC$的长的最小值为______。

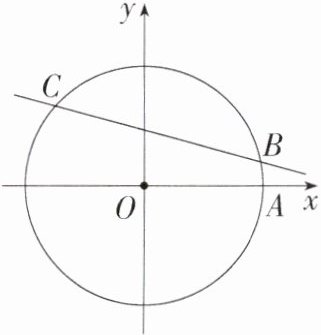
答案：
8.答案　24
解析　如图,连接OB,过O作OD⊥BC于点D.直线y=kx - 3k + 4=k(x - 3)+4,当x=3时,y=4,

∴直线y=kx - 3k + 4必过点(3,4),
∴最短的弦CB是过点(3,4)且与该圆直径垂直的弦,此时点D的坐标是(3,4),
∴OD=$\sqrt{3^2 + 4^2}=5$,
∵以原点O为圆心的圆过点A(13,0),
∴圆O的半径为13,
∴OB=13,
∴BD=$\sqrt{OB^2 - OD^2}=\sqrt{13^2 - 5^2}=12$,
∴BC=2BD=24,
∴BC的长的最小值为24.