《2025年5年中考3年模拟九年级数学全一册苏科版》

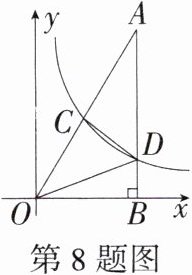
8. 「2025江苏宜兴外国语学校月考,」如图,已知平面直角坐标系$xOy$中,$Rt\triangle OAB的直角顶点B在x$轴的正半轴上,点$A$在第一象限,反比例函数$y= \frac{k}{x}(x＞0)的图像交OA于点C$,交$AB于点D$,连接$CD$,$OD$,若$OC:AC= 3:4$,$\triangle ACD的面积是8$,则$k$的值为( )

A.$\frac{63}{10}$
B.$\frac{20}{3}$
C.$\frac{36}{5}$
D.$\frac{69}{5}$

答案：
A　如图,过点C作CE⊥x轴于点E,则CE//AB,
∴△COE∽△AOB,S△COE/S△AOB = (OC/OA)²,

∵OC:AC = 3:4,
∴OC:OA = 3:7,S△COD:S△ACD = 3:4,
∴S△COE/S△AOB = 9/49,即S△AOB = 49/9S△COE,
∵△ACD的面积是8,
∴S△COD = 6,
∵反比例函数y = k/x(x＞0)的图像交OA于点C，交AB于点D,
∴S△COE = S△BOD = 1/2k,
∵S△BOD + S△AOD = S△AOB,
∴1/2k + 6 + 8 = 49/9×1/2k,解得k = 63/10.故选A.

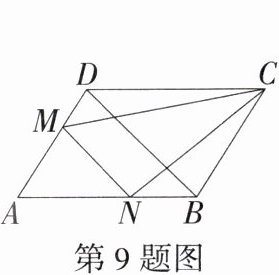
9. 等积变换法「2023江苏苏州高新区一模,」在中学数学中求一些图形面积时,经常用到“同底等高”“等底等高”等数学思想方法,我们称它为等积变换.如图,$BD为□ ABCD$的对角线,$M$、$N分别在AD$、$AB$上,且$\frac{AM}{AD}= \frac{AN}{AB}= \frac{2}{3}$,若$S_{\triangle DMC}= 3$,则$S_{\triangle BNC}+S_{\triangle AMN}= $______.

答案：
7
解析　如图,连接AC,过点C作CF⊥AD交AD的延长线于F,CE⊥AB交AB的延长线于E.

∵四边形ABCD是平行四边形，
∴S△ABC = S△ADC,
∴CF·AD = CE·AB,
∵AM/AD = AN/AB = 2/3,
∴MN//BD,
∴AD/DM = AB/BN,
∴CF·MD = CE·BN,
∴S△DMC = S△BNC = 3,
∴S△ACN = S△AMC = 6,
∴S▱ABCD = 18,
∴S△ABD = 1/2S▱ABCD = 9,
∵MN//BD,
∴△AMN∽△ADB,
∴S△AMN/S△ADB = (2/3)²,
∴S△AMN = 4,
∴S△BNC + S△AMN = 7.

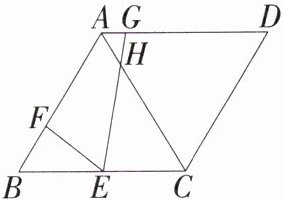
10. 「2025江苏徐州泉山期末,」如图,在菱形$ABCD$中,$\angle B= 60^{\circ}$,$BC= 6$,$E为BC$的中点,$F是AB$上一点,$G为AD$上一点,且$BF= 2$,$\angle FEG= 60^{\circ}$,$EG交AC于点H$,则$\frac{S_{\triangle BEF}}{S_{\triangle AGH}}$的值为______4.

答案： 4
解析
∵四边形ABCD是菱形，
∴AB//CD,CA平分∠BCD,
∵∠B = °,
∴∠BCD = 120°,
∴∠ACB = 60° = ∠B,
∵∠FEG = 60°,
∴∠BEF = 120° - ∠CEH = ∠CHE,
∴△BEF∽△CHE,
∴BF/CE = BE/CH,
∵E为BC的中点,
∴CE = BE = 3,
∴2/3 = 3/CH,解得CH = 4.5,
又
∵AC = BC = 6,
∴AH = AC - CH = 1.5,
∵AG//CE,
∴△AGH∽△CEH
∴AG/CE = AH/CH = 1/3,
∴AG = 1/3CE = 1,
∵BF = 2/3CE,△BEF∽△CHE,△AGH∽△CEH,
∴S△CEH = 9S△AGH,S△CEH = 9/4S△BEF,
∴9S△AGH = 9/4S△BEF,
∴S△BEF = 4S△AGH,
∴S△BEF/S△AGH = 4.

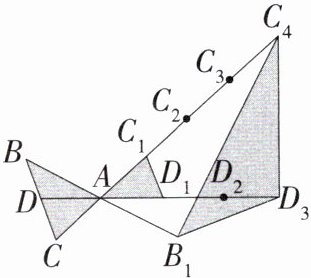
11. 几何直观「2024河北中考」如图,$\triangle ABC的面积为2$,$AD为BC$边上的中线,点$A$,$C_{1}$,$C_{2}$,$C_{3}是线段CC_{4}$的五等分点,点$A$,$D_{1}$,$D_{2}是线段DD_{3}$的四等分点,点$A是线段BB_{1}$的中点.
(1)$\triangle AC_{1}D_{1}$的面积为______.
(2)$\triangle B_{1}C_{4}D_{3}$的面积为______.

答案：

(1)1　
(2)7
解析　
(1)如图,连接B₁D₁、B₁D₂、B₁C₂、B₁C₃、C₃D₃,

∵△ABC的面积为2,AD为BC边上的中线,
∴S△ABD = S△ACD = 1/2S△ABC = 1/2×2 = 1,
∵点A,C₁,C₂,C₃是线段CC₄的五等分点,
∴AC = AC₁ = C₁C₂ = C₂C₃ = C₃C₄ = 1/5CC₄,
∵点A,D₁,D₂是线段DD₃的四等分点,
∴AD = AD₁ = D₁D₂ = D₂D₃ = 1/4DD₃,
∵点A是线段BB₁的中点,
∴AB = AB₁ = 1/2BB₁,
在△AC₁D₁和△ACD中,{AC₁ = AC,∠C₁AD₁ = ∠CAD,AD₁ = AD},
∴△AC₁D₁≌△ACD(SAS),
∴S△AC₁D₁ = S△ACD = 1,即△AC₁D₁的面积为1.
(2)在△AB₁D₁和△ABD中,{AB₁ = AB,∠B₁AD₁ = ∠BAD,AD₁ = AD},
∴△AB₁D₁≌△ABD(SAS),
∴S△AB₁D₁ = S△ABD = 1,∠B₁D₁A = ∠BDA,
∵∠BDA + ∠CDA = 180°,
∴∠B₁D₁A + ∠C₁D₁A = 180°,
∴C₁、D₁、B₁三点共线,
∴S△AB₁C₁ = S△AB₁D₁ + S△AC₁D₁ = 1 + 1 = 2,
∵AC₁ = C₁C₂ = C₂C₃ = C₃C₄,
∴S△AB₁C₄ = 4S△AB₁C₁ = 4×2 = 8,
∵AD₁ = D₁D₂ = D₂D₃,S△AB₁D₁ = 1,
∴S△AB₁D₃ = 3S△AB₁D₁ = 3×1 = 3,
在△AC₃D₃和△ACD中,AC₃/AC = 3 = AD₃/AD,∠C₃AD₃ = ∠CAD,
∴△C₃AD₃∽△CAD,
∴S△C₃AD₃/S△CAD = (AC₃/AC)² = 3² = 9,
∴S△C₃AD₃ = 9S△CAD = 9×1 = 9,
∵AC₁ = C₁C₂ = C₂C₃ = C₃C₄,
∴S△AC₄D₃ = 4/3S△C₃AD₃ = 4/3×9 = 12,
∴S△B₁C₄D₃ = S△AC₄D₃ + S△AB₁D₃ - S△AB₁C₄ = 12 + 3 - 8 = 7,
∴△B₁C₄D₃的面积为7.

1. 如图,在$\triangle ABC$中,$D$、$E$、$F$、$G$、$H$、$I均为\triangle ABC$三边的三等分点,$\triangle ABC的面积为9$,则六边形$DEFGHI$的面积为(C)
A.$1$
B.$3$
C.$6$
D.$8$

答案： C
∵H、G分别是AC和BC的三等分点,
∴CH = 1/3AC,CG = 1/3BC,
∴CH/CA = CG/CB = 1/3,
∵∠HCG = ∠ACB,
∴△CHG∽△CAB,
∴S△CHG/S△CAB = (CH/CA)² = 1/9,
∵△ABC的面积 = 9,
∴△CHG的面积 = 9×1/9 = 1,同理,△ADI的面积 = 1,△BEF的面积 = 1,
∴六边形DEFGHI的面积 = △ABC的面积 - △CHG的面积 - △ADI的面积 - △BEF的面积 = 9 - 1 - 1 - 1 = 6.故选C.

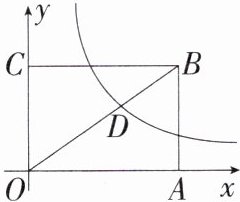
2. 「2025江苏扬州江都三中月考」如图,矩形$OABC的对角线OB与反比例函数y= \frac{9}{x}(x＞0)的图像交于点D$,且$\frac{OD}{OB}= \frac{3}{5}$,则矩形$OABC$的面积为______.

答案：
25
解析　过点D作DE⊥x轴于点E,如图,设OE = a,DE = b,则点D(a,b),

∵点D在反比例函数y = 9/x(x＞0)的图像上,
∴ab = 9,
∵四边形OABC为矩形,
∴∠OAB = 90°,
∵DE⊥x轴,
∴DE//AB,
∴△ODE∽△OBA,
∴OE/OA = DE/AB = OD/OB,
∵OD/OB = 3/5,
∴OA = 5/3a,AB = 5/3b,
∴S矩形OABC = OA·AB = 5/3a·5/3b = 25/9ab,
∵ab = 9,
∴S矩形OABC = 25.

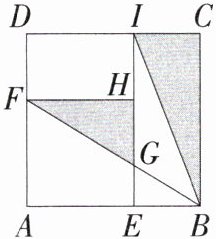
3. 「2024江苏苏州高新区第一中学期末」如图,点$E是正方形ABCD的边AB$上的黄金分割点,且$AE＞EB$,以$AE为边作正方形AEHF$,延长$EH交CD于点I$,连接$BF交EI于点G$,连接$BI$,则$S_{\triangle BCI}:S_{\triangle FGH}$为______(√5 + 1)/2.

答案： (√5 + 1)/2
解析
∵四边形ABCD是正方形,
∴BC = CD = DA = AB,
∵点E是正方形ABCD的边AB上的黄金分割点,且AE＞EB,
∴AE/AB = BE/AE = (√5 - 1)/2,
∵四边形AEHF是正方形,
∴EH = HF = FA = AE,FH//AE,
∴△FHG∽△BEG,
∴GH/GE = FH/BE,
∴GH/HE = FH/(FH + BE) = AE/(AE + BE) = AE/AB = (√5 - 1)/2,
∴GH = (√5 - 1)/2HE = (√5 - 1)/2AE,
∵∠C = ∠CBE = ∠BEI = 90°,
∴四边形BCIE是矩形,
∴IC = BE,
∴S△BCI:S△FGH = (1/2BC·IC)/(1/2FH·HG) = (AB·BE)/(AE·HG) = (BE/AE)·(AB/HG) = (√5 - 1)/2·AB/((√5 - 1)/2AE) = (√5 - 1)/2·1/((√5 - 1)/2·(√5 - 1)/2) = 2/(√5 - 1) = (√5 + 1)/2.