《2025年5年中考3年模拟九年级数学全一册苏科版》

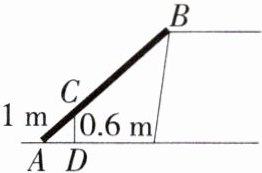
1.如图,把一根长为4.5m的竹竿AB斜靠在石坝旁,量出竿长1m处离地面的高度为0.6m,则石坝的高度为( )


A.2.7m
B.3.6m
C.2.8m
D.2.1m

答案：
A 如图,过点B作BF⊥AD于点F.
∵CD⊥AD,BF⊥AD,
∴CD//BF,
∴△ACD∽△ABF,
∴$\frac{DC}{BF}=\frac{AC}{AB}$,
∴$\frac{0.6}{BF}=\frac{1}{4.5}$,解得BF=2.7 m,即石坝的高度为2.7 m.

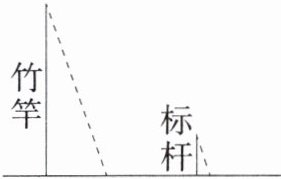
2.新考向数学文化「2024江苏无锡宜兴一模」《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣：“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何？”意思是：有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的标杆(如图所示),它的影长为五寸,则竹竿的长为______(提示：1丈= 10尺,1尺= 10寸)。

四丈五尺

答案： 四丈五尺 解析 设竹竿的长为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,标杆的影长=五寸=0.5尺,
∴$\frac{x}{15}=\frac{1.5}{0.5}$,解得x=45,45尺=四丈五尺.

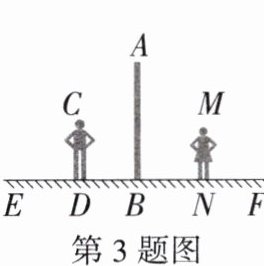
3.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为______。

答案：
3 m 解析 如图,
∵CD//AB//MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴$\frac{CD}{AB}=\frac{DE}{BE}$,$\frac{FN}{FB}=\frac{MN}{AB}$,即$\frac{1.8}{AB}=\frac{1.8}{1.8+BD}$,$\frac{1.5}{1.5+2.7 - BD}=\frac{1.5}{AB}$,解得AB=3 m.故路灯的高为3 m.

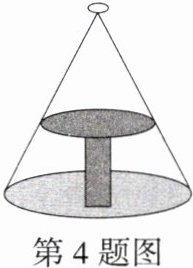
4.学科特色教材变式PS5练习12「2025湖南邵阳七中段考」如图所示的是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成的示意图(圆形)。已知桌面直径为1.2米,桌面离地面1米。若灯泡离地面3米,则地面上阴影部分的面积为______(结果保留π)。

答案：
0.81π平方米 解析 如图,设C,D分别是桌面和地面影子的圆心,连接OD,CB,DA,则CB//AD,O、C、D在一条直线上,
∴△OBC∽△OAD,
∴$\frac{CB}{AD}=\frac{OC}{OD}$.
∵OD=3米,CD=1米,
∴OC=OD - CD=3 - 1=2(米),又BC=$\frac{1}{2}$×1.2=0.6(米),
∴$\frac{0.6}{AD}=\frac{2}{3}$,
∴AD=0.9米,
∴$S_{⊙D}=π×0.9^{2}=0.81π$(平方米),
∴地面上阴影部分的面积为0.81π平方米.

5.「2023江苏南京外国语学校淮安分校期中,☆☆」如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上。已知铁塔底座宽CD= 12m,塔影长DE= 18m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子在平地上,两人的影长分别为2m和1m,则塔高AB= ______。

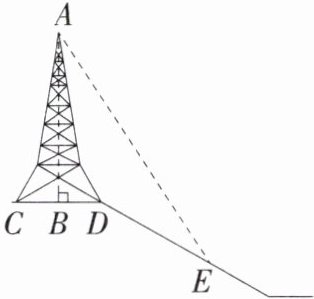
答案：
24 m 解析 如图,过D作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G.由题意得$\frac{DF}{DE}=\frac{1.6}{2}$,
∴DF=DE×1.6÷2=14.4(m).易知四边形BDFG为矩形,
∴GF=BD=$\frac{1}{2}$CD=6 m,由题意得$\frac{AG}{GF}=\frac{1.6}{1}$,
∴AG=1.6×6=9.6(m).
∴AB=14.4+9.6=24(m).

6.「☆☆」九年级某班开展数学活动,活动内容为测量如图所示的电线杆AB的高度。在太阳光的照射下,电线杆影子的一部分(BE)落在地面上,另一部分(EF)落在斜坡上,站在水平面上的小明的影子为DG,已知∠FEH= 30°,CD= 1.6m,DG= 0.8m,BE= 2.1m,EF= 1.7m,则电线杆的高约为______m。(精确到0.1,参考数据：$\sqrt{2}\approx1.41$,$\sqrt{3}\approx1.73$)

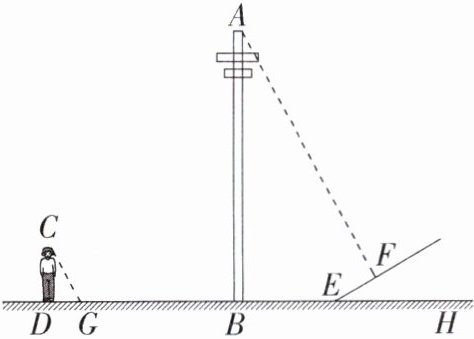
答案：
8.0 解析 如图,延长AF交BH于点N,过点F作FM⊥BH于点M,
∵∠FEH=30°,EF=1.7 m,
∴FM=$\frac{1}{2}$EF=0.85 m,
∴EM=$\sqrt{EF^{2}-FM^{2}}$≈1.47 m.易知△FMN∽△CDG,
∴$\frac{FM}{CD}=\frac{MN}{DG}$,
∵CD=1.6 m,DG=0.8 m,
∴$\frac{0.85}{1.6}=\frac{MN}{0.8}$,
∴MN=0.425 m,
∵BE=2.1 m,
∴BN=2.1+1.47+0.425≈4.0(m),易知△ABN∽△CDG,
∴$\frac{AB}{BN}=\frac{CD}{DG}$,
∴$\frac{AB}{4.0}=\frac{1.6}{0.8}$,
∴AB=8.0 m,即电线杆的高约为8.0 m.