《2025年5年中考3年模拟九年级数学全一册苏科版》

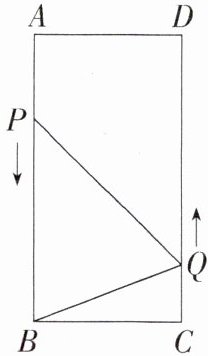
8.学科特色分类讨论思想「2024江苏苏州工业园区星湾学校月考,☆☆☆」如图,在矩形$ABCD$中,$AB = 16cm$,$BC = 6cm$,动点$P$,$Q分别以3cm/s$,$2cm/s的速度从点A$,$C$同时出发,沿规定路线移动.
(1)若点$P从点A移动到点B$停止,点$Q随点P$的停止而停止移动,则经过多长时间,$P$,$Q两点之间的距离是10cm$?
(2)连接$BQ$,若点$P沿着AB→BC→CD$移动,点$Q从点C移动到点D$停止,点$P随点Q$的停止而停止移动,则经过多长时间,$△PBQ的面积为12cm^{2}$?

答案：
(1)如图,过点P作PE⊥CD于E,设经过xs,点P和点Q之间的距离是10cm，由勾股定理得EQ²+PE²=PQ²,即(16−2x−3x)²+6²=10²,
∴x₁=$\frac{8}{5}$,x₂=$\frac{24}{5}$,
∴经过$\frac{8}{5}$s或$\frac{24}{5}$s,P,Q两点之间的距离是10cm；
(2)设经过ys,△PBQ的面积为12cm²,分三种情况讨论:①当0≤y＜$\frac{16}{3}$时,PB=(16−3y)cm,此时S△PBQ=$\frac{1}{2}$PB·BC=12cm²,
∴$\frac{1}{2}$×(16−3y)×6=12,解得y=4;②当$\frac{16}{3}$≤y≤$\frac{22}{3}$时,BP=(3y−16)cm,QC=2ycm,此时S△PBQ=$\frac{1}{2}$BP·CQ=12cm²,
∴$\frac{1}{2}$(3y−16)×2y=12,解得y₁=6,y₂=−$\frac{2}{3}$(舍去);③当$\frac{22}{3}$＜y≤8时,QP=CQ−PC=2y−(3y−22)=(22−y)cm,此时S△PBQ=$\frac{1}{2}$QP·CB=12cm²,
∴$\frac{1}{2}$(22−y)×6=12,解得y=18(舍去).综上所述，经过4s或6s,△PBQ的面积为12cm².

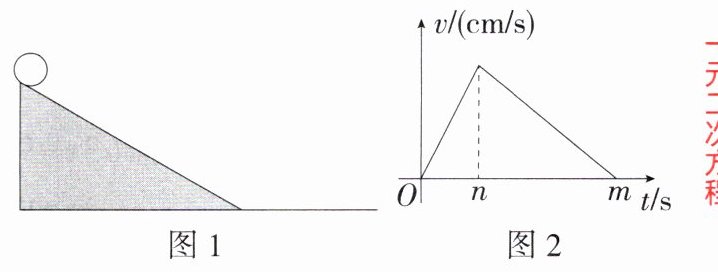
9.新课标推理能力跨物理匀变速运动如图1,一小球从斜面顶端由静止开始沿斜面下滚,呈匀加速运动状态,速度每秒增加$2cm/s$;然后在水平地面上继续滚动,呈匀减速运动状态,滚动速度每秒减小$0.8cm/s$.速度$v(cm/s)与时间t(s)$的关系如图2中的实线所示.(提示:根据物理学知识可知,物体匀加速运动时的路程$s= 平均速度\overline{v}×时间t$,$\overline{v}= (v_{0}+v_{t})÷2$,其中$v_{0}(cm/s)$是开始时的速度,$v_{t}(cm/s)是t$秒时的速度,匀减速运动时的路程和平均速度类似可得)
(1)当$n = 8$时,求解下面问题.
①求$m$的值;
②写出滚动的路程$s(cm)关于时间t(s)$的函数解析式.
(2)若小球滚动的最大路程为$350cm$,则小球在水平地面上滚动了多长时间?

答案：
(1)①根据题意得2n−0.8(m−n)=0,
∴m=3.5n,当n=8时,m=3.5×8=28；②当0≤t≤8时,v=2t,
∴s=$\frac{1}{2}$v·t=$\frac{1}{2}$×2t·t,
∴s=t²;当8＜t≤28时,v=2×8−0.8(t−8)=−0.8t+22.4,
∴s=8×8+$\frac{1}{2}$(2×8−0.8t+22.4)(t−8),
∴s=−0.4t²+22.4t−89.6.
∴滚动的路程s(cm)关于滚动时间t(s)的函数解析式为s=$\begin{cases}t^{2}&(0\leq t\leq8)\\-0.4t^{2}+22.4t - 89.6&(8\lt t\leq28)\end{cases}$；
(2)
∵m=3.5n,且小球滚动的最大路程为350cm,
∴n·n+$\frac{1}{2}$×2n·(m−n)=350,
∴n²=100,解得n₁=10,n₂=−10(不符合题意，舍去),
∴m−n=3.5n−n=2.5n=2.5×10=25(秒).答:小球在水平地面上滚动了25秒.