《2025年5年中考3年模拟九年级数学全一册苏科版》

10.新考向代数推理「2025江苏南京外国语学校淮安分校月考,★☆」设a,b,c是△ABC的三条边,且$\frac{a-b}{b}= \frac{b-c}{c}= \frac{c-a}{a},$△ABC为何种三角形？并说明理由。

答案： 解析 △ABC为等边三角形.理由如下:设$\frac{a-b}{b}=\frac{b-c}{c}=\frac{c-a}{a}=k$,则a-b=bk,b-c=ck,c-a=ak,
∴(a+b+c)k=0,
∵a,b,c是△ABC的三条边,
∴a≠0,b≠0,c≠0,a+b+c≠0,
∴k=0,则a-b=0,b-c=0,c-a=0,
∴a=b=c,
∴△ABC为等边三角形.

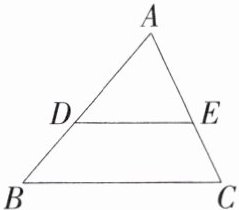
11.「★☆」如图所示,在△ABC中,$\frac{AD}{DB}= \frac{AE}{EC},$AB= 12,AE= 6,EC= 4。
(1)求AD的长。
(2)试说明$\frac{DB}{AB}= \frac{EC}{AC}$成立。
]

答案： 解析
(1)
∵$\frac{AD}{DB}=\frac{AE}{EC}$,
∴$\frac{AD}{12-AD}=\frac{6}{4}$,
∴$AD=\frac{36}{5}$.
(2)证明:
∵$\frac{AD}{DB}=\frac{AE}{EC}$,
∴$\frac{AD}{BD}+1=\frac{AE}{EC}+1$,
∴$\frac{AD+DB}{DB}=\frac{AE+EC}{EC}$,即$\frac{AB}{DB}=\frac{AC}{EC}$,
∴$\frac{DB}{AB}=\frac{EC}{AC}$.

12.新课标运算能力已知$\frac{a}{b}= \frac{c}{d}= \frac{e}{f}= 2,且k= \frac{a+3c-e}{b+3d-f},$若x_1,x_2是方程x^2-3x+k-4= 0的两根,求3x_1^2+2x_2^2-3x_1+3的值。

答案： 解析
∵$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=2$,
∴a=2b,c=2d,e=2f,
∴$k=\frac{a+3c-e}{b+3d-f}=\frac{2b+6d-2f}{b+3d-f}=2$.
∴原方程为$x^{2}-3x-2=0$.
∵$x_{1},x_{2}$是方程$x^{2}-3x-2=0$的两根,
∴$x_{1}+x_{2}=3$,$x_{1}x_{2}=-2$,$x_{1}^{2}-3x_{1}-2=0$.
∴$3x_{1}^{2}+2x_{2}^{2}-3x_{1}+3=2(x_{1}^{2}+x_{2}^{2})+x_{1}^{2}-3x_{1}+3=2(x_{1}+x_{2})^{2}-4x_{1}x_{2}+2+3=2×3^{2}-4×(-2)+5=31$.

13.新课标推理能力「2025江苏苏州中学月考」已知△ABC的三边长a,b,c满足(a-c):(a+b):(c-b)= -2:7:1,且a+b+c= 24。
(1)求a,b,c的值。
(2)判断△ABC的形状。

答案： 解析
(1)设a-c=-2k,a+b=7k,c-b=k,
∴a=7k-b,c=k+b,
∴a-c=7k-b-k-b=6k-2b,
∴6k-2b=-2k,即8k-2b=0.
∵a+b+c=24,
∴7k-b+b+k+b=24,即8k+b=24.由$\begin{cases}8k-2b=0,\\8k+b=24\end{cases}$解得$\begin{cases}k=2,\\b=8,\end{cases}$
∴a=6,c=10.故a,b,c的值分别为6,8,10.
(2)
∵$a^{2}+b^{2}=6^{2}+8^{2}=100=10^{2}=c^{2}$,
∴△ABC是直角三角形.