《2025年5年中考3年模拟九年级数学全一册苏科版》

1. 「2024 云南中考」某校九年级学生参加社会实践,学习编织圆锥型工艺品.若这种圆锥的母线长为 40 厘米,底面圆的半径为 30 厘米,则该圆锥的侧面积为(C)
A.$700\pi$ 平方厘米
B.$900\pi$ 平方厘米
C.$1200\pi$ 平方厘米
D.$1600\pi$ 平方厘米

答案： C
∵ 圆锥的底面圆周长为2π×30 = 60π厘米，
∴ 圆锥的侧面积为$\frac{1}{2}×60π×40 = 1200π$平方厘米，故选C。

2. 「2024 江苏宿迁中考」已知圆锥的底面圆半径为 3,母线长为 12,则其侧面展开扇形的圆心角的度数为90°。

答案： 答案 90
解析 设圆锥的侧面展开扇形的圆心角的度数为$n^{\circ}$，由题意得$\frac{nπ×12}{180} = 2π×3$，解得n = 90。

3. 如图所示的是某几何体的三视图,根据图中尺寸计算该圆锥的全面积为$12π\ \text{cm}^2$。

答案： 答案 $12π\ \text{cm}^2$
解析 由三视图知该几何体为圆锥，其高为$2\sqrt{3}\ \text{cm}$，底面圆半径为2 cm，
∴ 圆锥的母线长为$\sqrt{2^2+(2\sqrt{3})^2} = 4(\text{cm})$，
∴ 圆锥的全面积$= π×2^2 + π×2×4 = 12π(\text{cm}^2)$。

4. 「2024 江苏徐州中考」将圆锥的侧面沿一条母线剪开后展平,所得扇形的面积为 $4\pi \text{ cm}^2$,圆心角 $\theta$ 为 $90^{\circ}$,则圆锥的底面圆的半径为1 cm。

答案： 答案 1 cm
解析 设扇形的半径为R cm，弧长为l cm，由题意得$\frac{90π×R^2}{360} = 4π$，解得R = 4(负值舍去)，则$\frac{1}{2}l×4 = 4π$，解得l = 2π，
∴ 圆锥的底面圆的半径为2π÷2π = 1(cm)。

5. 若一个圆锥的侧面展开图是一个半圆,它的高为 $4\sqrt{3} \text{ cm}$,求该圆锥的全面积。

答案： 解析 设圆锥母线长为l cm，底面圆的半径为r cm，根据题意得$2πr = \frac{180·π·l}{180}$，
∴ l = 2r。
∵ $r^2+(4\sqrt{3})^2 = l^2$，
∴ $r^2+(4\sqrt{3})^2 = 4r^2$，解得r = 4(舍负)，
∴ l = 8，
∴ 圆锥的全面积$= π×4^2 + π×4×8 = 48π(\text{cm}^2)$。

6. 「2022 四川绵阳中考,☆☆」如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位：mm)。电镀时,如果每平方米用锌 0.1 千克,电镀 1000 个这样的锚标浮筒,需要多少千克锌？($\pi$ 取 3.14)(A)
A.282.6 千克
B.282600000 千克
C.357.96 千克
D.357960000 千克

答案： A 由题图可知圆锥的底面圆的半径为0.3 m，圆锥的高为0.4 m，则圆锥的母线长为$\sqrt{0.3^2 + 0.4^2} = 0.5(\text{m})$。
∴ 圆锥的侧面积$= π×0.3×0.5 = 0.15π(\text{m}^2)$，
∵ 圆柱的高为1 m，
∴ 圆柱的侧面积$= 2π×0.3×1 = 0.6π(\text{m}^2)$，
∴ 锚标浮筒的表面积$= 2×0.15π + 0.6π = 0.9π(\text{m}^2)$，
∵ 每平方米用锌0.1 kg，
∴ 1000个这样的锚标浮筒需用锌$1000×0.9π×0.1 = 90π = 282.6(\text{kg})$。故选A。

7. 「2023 内蒙古赤峰中考,☆☆」某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆周长为 $20\pi \text{ cm}$,母线 $AB$ 长为 30 cm。为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点 $A$ 处开始,绕侧面一周又回到点 $A$ 的彩带(彩带宽度忽略不计),则这条彩带的最短长度是( )


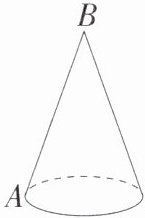
A.30 cm
B.$30\sqrt{3} \text{ cm}$
C.60 cm
D.$20\pi \text{ cm}$

答案：
B 将圆锥的侧面展开如图所示。

∵ 圆锥的底面圆周长为20π cm，
∴ 圆锥的侧面展开图的扇形的弧长为20π cm。设扇形的圆心角为$n^{\circ}$，
∴ $\frac{nπ×30}{180} = 20π$，解得n = 120，
∴ ∠ABA' = 120°。连接AA'，作BC⊥AA'于点C，
∵ AB = A'B，
∴ ∠BAA' = 30°，
∴ $BC = \frac{1}{2}AB = 15\ \text{cm}$，
∴ $AC = 15\sqrt{3}\ \text{cm}$，
∴ $AA' = 2AC = 30\sqrt{3}\ \text{cm}$，
∴ 这条彩带的最短长度是$30\sqrt{3}\ \text{cm}$。

8. 「2023 四川自贡中考,☆☆」如图,小珍同学用半径为 8 cm,圆心角为 $100^{\circ}$ 的扇形纸片,制作一个底面半径为 2 cm 的圆锥侧面,则圆锥上粘贴部分的面积是______$\text{cm}^2$。

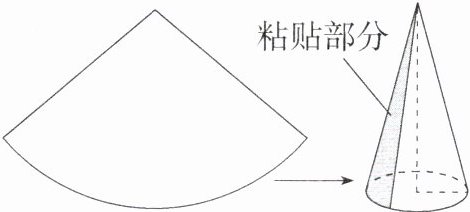
$\frac{16π}{9}$

答案： 答案 $\frac{16π}{9}$
解析 根据圆锥的底面半径为2 cm，可得其底面周长为4π cm，
∵ 扇形弧长为$\frac{100π×8}{180} = \frac{40}{9}π\ \text{cm}$，
∴ 粘贴部分的弧长为$\frac{40}{9}π - 4π = \frac{4}{9}π\ \text{cm}$，
∴ 圆锥上粘贴部分的面积是$\frac{1}{2}×\frac{4}{9}π×8 = \frac{16π}{9}(\text{cm}^2)$。