第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1.北京时间 2024 年 8 月 12 日,2024 年巴黎奥运会顺利闭幕,中国体育代表团共收获 40 金 27 银 24 铜,位于金牌榜第一、奖牌榜第二.其中,获奖牌榜前 5 的为 126(美国)、91(中国)、45(日本)、53(澳大利亚)、64(法国),则这五个国家奖牌总数的极差是____
81
.
答案:
81 解析 由极差的定义可得这五个国家奖牌总数的极差为126-45=81.
2.若一组数据 3,7,9,a,1 的平均数是 5,中位数是 m,极差是 n,则 m - n =
-3
.
答案:
-3 解析
∵平均数为5,
∴$\frac{3+7+9+a+1}{5}=5$,解得a=5,
∴极差n=9-1=8.
∵这组数据按从小到大的顺序排列为1,3,5,7,9,
∴中位数为5,即m=5.
∴m-n=5-8=-3.
∵平均数为5,
∴$\frac{3+7+9+a+1}{5}=5$,解得a=5,
∴极差n=9-1=8.
∵这组数据按从小到大的顺序排列为1,3,5,7,9,
∴中位数为5,即m=5.
∴m-n=5-8=-3.
3.「2024 黑龙江龙东地区中考」一组数据 2,3,3,4,则这组数据的方差为 (
A.1
B.0.8
C.0.6
D.0.5
D
)A.1
B.0.8
C.0.6
D.0.5
答案:
D 这组数据的平均数是(2+3+3+4)÷4=3,则这组数据的方差为$\frac{1}{4}×[(2-3)^{2}+2×(3-3)^{2}+(4-3)^{2}]=0.5$.故选D.
4.「2024 云南中考」甲、乙、丙、丁四名运动员参加射击项目选拔赛,每人 10 次射击成绩的平均数$\overline {x}$(单位:环)和方差$s^{2}$如下表所示:
| | 甲 | 乙 | 丙 | 丁 |
| $\overline {x}$ | 9.9 | 9.5 | 8.2 | 8.5 |
| $s^{2}$ | 0.09 | 0.65 | 0.16 | 2.85 |
根据表中数据,从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择 (
A.甲
B.乙
C.丙
D.丁
| | 甲 | 乙 | 丙 | 丁 |
| $\overline {x}$ | 9.9 | 9.5 | 8.2 | 8.5 |
| $s^{2}$ | 0.09 | 0.65 | 0.16 | 2.85 |
根据表中数据,从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择 (
A
)A.甲
B.乙
C.丙
D.丁
答案:
A 由题表可知射击成绩的平均数最大的是甲,射击成绩的方差最小的也是甲,
∴从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择甲,故选A.
∴从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择甲,故选A.
5.「2025 江苏南京外国语学校段考」小明同学用$s^{2}= \frac {1}{10}[(x_{1}-8)^{2}+(x_{2}-8)^{2}+... +(x_{10}-8)^{2}]计算一组数据x_{1},x_{2},...,x_{10}$的方差,那么$x_{1}+x_{2}+... +x_{10}$=
80
.
答案:
80 解析 由$s^{2}=\frac{1}{10}[(x_{1}-8)^{2}+(x_{2}-8)^{2}+\cdots+(x_{10}-8)^{2}]$可知这10个数据的平均数为8,则$x_{1}+x_{2}+\cdots+x_{10}=8×10=80$.
6.「2024 江苏常州中考」小丽进行投掷标枪训练,总共投掷 10 次,前 9 次标枪的落点如图所示,记录成绩(单位:m),此时这组成绩的平均数是 20 m,方差是$s_{1}^{2}m^{2}$.若第 10 次投掷标枪的落点恰好在线上,且投掷结束后这组成绩的方差是$s_{2}^{2}m^{2}$,则$s_{1}^{2}$
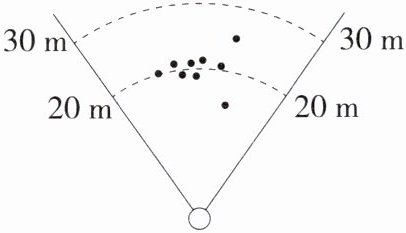
>
$s_{2}^{2}$(填“>”“=”或“<”).
答案:
> 解析 由题意可得,前9次成绩的平均数和10次成绩的平均数相同,均为20m,
∵第10次投掷标枪的落点恰好在20m线上,
∴$s_{2}^{2}=\frac{9}{10}s_{1}^{2}$,
∴$s_{1}^{2}>s_{2}^{2}$.
∵第10次投掷标枪的落点恰好在20m线上,
∴$s_{2}^{2}=\frac{9}{10}s_{1}^{2}$,
∴$s_{1}^{2}>s_{2}^{2}$.
7.某学校开展了该校八年级部分学生的综合素质测评活动,随机选取了该校八年级的 50 名学生进行测评,统计数据如表:
| 测评成绩/分 | 80 | 85 | 90 | 95 | 100 |
| 人数 | 5 | 10 | 10 | 20 | 5 |
(1)这 50 名学生的测评成绩的平均数是
(2)若该校八年级共有学生 300 名,测评成绩在 90 分及以上的为优秀,试估计该校八年级优秀学生共有多少名.
| 测评成绩/分 | 80 | 85 | 90 | 95 | 100 |
| 人数 | 5 | 10 | 10 | 20 | 5 |
(1)这 50 名学生的测评成绩的平均数是
91
分,众数是95
分,中位数是92.5
分,方差是34
.(2)若该校八年级共有学生 300 名,测评成绩在 90 分及以上的为优秀,试估计该校八年级优秀学生共有多少名.
210名
答案:
(1)91;95;92.5;34 解析
(1)
∵测评成绩为95分的人数最多,
∴众数是95分;将成绩从小到大排列,则中位数是$\frac{90+95}{2}=92.5$(分);平均数是(80×5+85×10+90×10+95×20+100×5)÷50=91(分);方差=$\frac{1}{50}[5×(80-91)^{2}+10×(85-91)^{2}+10×(90-91)^{2}+20×(95-91)^{2}+5×(100-91)^{2}]=34$.故答案为91;95;92.5;34.
(2)210名 解析
(2)$300×\frac{10+20+5}{50}=210$(名).故该校八年级优秀学生约有210名.
(1)91;95;92.5;34 解析
(1)
∵测评成绩为95分的人数最多,
∴众数是95分;将成绩从小到大排列,则中位数是$\frac{90+95}{2}=92.5$(分);平均数是(80×5+85×10+90×10+95×20+100×5)÷50=91(分);方差=$\frac{1}{50}[5×(80-91)^{2}+10×(85-91)^{2}+10×(90-91)^{2}+20×(95-91)^{2}+5×(100-91)^{2}]=34$.故答案为91;95;92.5;34.
(2)210名 解析
(2)$300×\frac{10+20+5}{50}=210$(名).故该校八年级优秀学生约有210名.
8.已知一组数据 82,84,85,89,80,94,76,用计算器计算这组数据的方差约为(精确到 0.01) (
A.37.53
B.25.48
C.29.92
D.5.47
C
)A.37.53
B.25.48
C.29.92
D.5.47
答案:
C 用计算器计算这组数据的方差约为29.92.故选C.
查看更多完整答案,请扫码查看


