第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
10.「2024黑龙江牡丹江中考」已知一组正整数a,1,b,b,3有唯一众数8,中位数是5,则这一组数据的平均数为
5
.
答案:
答案 5 解析
∵这组数据有唯一众数8,
∴b为8,
∵中位数是5,
∴a是5,
∴这一组数据的平均数为$\frac{1 + 3 + 5 + 8 + 8}{5}$ = 5.
∵这组数据有唯一众数8,
∴b为8,
∵中位数是5,
∴a是5,
∴这一组数据的平均数为$\frac{1 + 3 + 5 + 8 + 8}{5}$ = 5.
11.若一组数据1,2,3,4,x的方差与另一组数据2020,2021,2022,2023,2024的方差相等,则x的值为
0或5
.
答案:
答案 0或5 解析
∵一组数据1,2,3,4,x的方差与另一组数据2020,2021,2022,2023,2024的方差相等,
∴这组数据可能是1,2,3,4,5或0,1,2,3,4,
∴x = 0或5.
∵一组数据1,2,3,4,x的方差与另一组数据2020,2021,2022,2023,2024的方差相等,
∴这组数据可能是1,2,3,4,5或0,1,2,3,4,
∴x = 0或5.
12.「2025江苏苏州吴江期中」(8分)已知一组数据:9,x,y,8,7,11,7,6的平均数为7,其中y-x= 2,求x,y的值.
答案:
解析
∵9,x,y,8,7,11,7,6的平均数为7,
∴$\frac{9 + x + y + 8 + 7 + 11 + 7 + 6}{8}$ = 7,故x + y = 8,由$\begin{cases} x + y = 8, \\ y - x = 2 \end{cases}$解得$\begin{cases} x = 3, \\ y =5. \end{cases}$
∵9,x,y,8,7,11,7,6的平均数为7,
∴$\frac{9 + x + y + 8 + 7 + 11 + 7 + 6}{8}$ = 7,故x + y = 8,由$\begin{cases} x + y = 8, \\ y - x = 2 \end{cases}$解得$\begin{cases} x = 3, \\ y =5. \end{cases}$
13.「2023江苏扬州仪征期中」(10分)某食品商店将甲、乙、丙3种糖果的质量按5:4:1配置成一种什锦糖果,已知甲、乙、丙三种糖果的单价分别为16元、20元、27元.若将这种什锦糖果的单价定为这三种糖果单价的算术平均数,你认为合理吗?如果合理,请说明理由;如果不合理,请求出该什锦糖果合理的单价.
答案:
解析 这样定价不合理.加权平均数 = 16×$\frac{5}{10}$ + 20×$\frac{4}{10}$ + 27×$\frac{1}{10}$ = 18.7(元),算术平均数 = $\frac{16 + 20 + 27}{3}$ = 21(元),
∵21 > 18.7,
∴将这种什锦糖果的单价定为这三种糖果单价的算术平均数不合理,该什锦糖果合理的单价为18.7元.
∵21 > 18.7,
∴将这种什锦糖果的单价定为这三种糖果单价的算术平均数不合理,该什锦糖果合理的单价为18.7元.
14.「2024江苏无锡新吴二模」(13分)甲、乙两校参加市英语口语比赛,两校参赛人数相等.比赛成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,组委会将甲、乙两所学校的成绩整理并绘制成如图所示的统计图,已知乙学校有11人的成绩是A等级.根据提供的信息,解答问题.
(1)将甲校的成绩统计图补充完整.
(2)补全下面的表格.
|学校|平均分|中位数|众数|
|甲|87.6| | |
|乙|87.6| | |
(3)从中位数或众数的角度对甲、乙两所学校的成绩做出评价,并说明理由.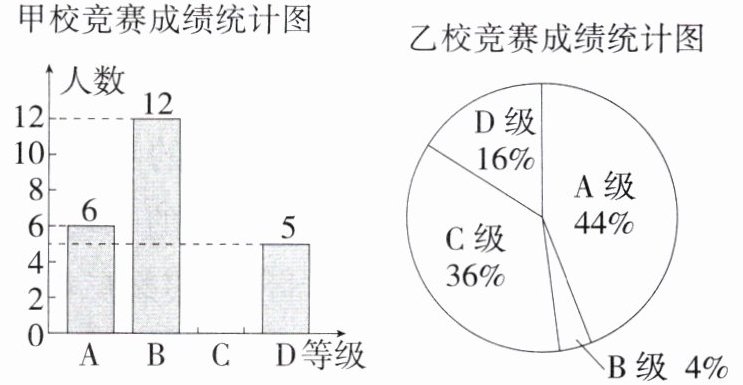
(1)将甲校的成绩统计图补充完整.
(2)补全下面的表格.
|学校|平均分|中位数|众数|
|甲|87.6| | |
|乙|87.6| | |
(3)从中位数或众数的角度对甲、乙两所学校的成绩做出评价,并说明理由.

答案:
解析
(1)
∵乙校有11人的成绩是A等级,占44%,
∴参赛人数为11÷44% = 25,
∵两校参赛人数相等,
∴甲校C级的人数为25 - (6 + 12 + 5)=2,将甲校竞赛成绩统计图补充完整如下:
(2)甲校成绩的中位数位于B级,即中位数为90分,乙校成绩的中位数位于C级,即中位数为80分,
∵甲校成绩中B级的人数最多,有12人,
∴甲校成绩的众数为90分,
∵乙校成绩中A级占44%,是比例最大的,
∴乙校成绩的众数为100分.
(3)从中位数看,甲校成绩的中位数高于乙校的中位数,所以甲校成绩好于乙校;从众数看,乙校成绩的众数高于甲校の众数,所以乙校成绩好于甲校.
解析
(1)
∵乙校有11人的成绩是A等级,占44%,
∴参赛人数为11÷44% = 25,
∵两校参赛人数相等,
∴甲校C级的人数为25 - (6 + 12 + 5)=2,将甲校竞赛成绩统计图补充完整如下:

(2)甲校成绩的中位数位于B级,即中位数为90分,乙校成绩的中位数位于C级,即中位数为80分,
∵甲校成绩中B级的人数最多,有12人,
∴甲校成绩的众数为90分,
∵乙校成绩中A级占44%,是比例最大的,
∴乙校成绩的众数为100分.
(3)从中位数看,甲校成绩的中位数高于乙校的中位数,所以甲校成绩好于乙校;从众数看,乙校成绩的众数高于甲校の众数,所以乙校成绩好于甲校.
15.(14分)在某旅游景区上山的一条小路上有一些断断续续的台阶.如图所示的是其中的甲、乙两段台阶路的示意图,其中图中的数字表示每一级台阶的高度(单位:cm).请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.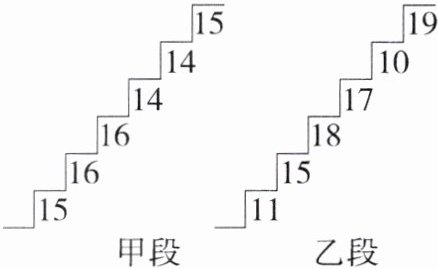
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.

答案:
解析
(1)$\overline{x}_{甲}$ = $\frac{1}{6}$×(15 + 16 + 16 + 14 +14 + 15)=15(cm),$\overline{x}_{乙}$ = $\frac{1}{6}$×(11 + 15 + 18 + 17 + 10 + 19)=15(cm);甲段的中位数为(15 + 15)÷2 = 15(cm),乙段的中位数为(15 + 17)÷2 = 16(cm);$s_{甲}^{2}$ = $\frac{1}{6}$×[(15 - 15)²+(16 - 15)²+(16 - 15)²+(14 - 15)²+(14 - 15)²+(15 - 15)²]=$\frac{2}{3}$(cm²),$s_{乙}^{2}$ = $\frac{1}{6}$×[(11 - 15)²+(15 - 15)²+(18 - 15)²+(17 - 15)²+(10 - 15)²+(19 - 15)²]=$\frac{35}{3}$(cm²);甲段的极差为16 - 14 = 2(cm),乙段的极差为19 - 10 = 9(cm).
∴相同点是两段台阶路每一级台阶高度的平均数相同,不同点是两段台阶路每一级台阶高度的中位数、方差和极差均不同.
(2)甲段台阶路走起来更舒服.理由如下:
∵它的每一级台阶高度的差较小,
∴台阶高度落差不大,走起来更舒服.
(3)每一级台阶高度均修整为15cm(原数据的平均数),使得方差为0cm²,此时游客行走最方便.(答案不唯一,合理即可)
(1)$\overline{x}_{甲}$ = $\frac{1}{6}$×(15 + 16 + 16 + 14 +14 + 15)=15(cm),$\overline{x}_{乙}$ = $\frac{1}{6}$×(11 + 15 + 18 + 17 + 10 + 19)=15(cm);甲段的中位数为(15 + 15)÷2 = 15(cm),乙段的中位数为(15 + 17)÷2 = 16(cm);$s_{甲}^{2}$ = $\frac{1}{6}$×[(15 - 15)²+(16 - 15)²+(16 - 15)²+(14 - 15)²+(14 - 15)²+(15 - 15)²]=$\frac{2}{3}$(cm²),$s_{乙}^{2}$ = $\frac{1}{6}$×[(11 - 15)²+(15 - 15)²+(18 - 15)²+(17 - 15)²+(10 - 15)²+(19 - 15)²]=$\frac{35}{3}$(cm²);甲段的极差为16 - 14 = 2(cm),乙段的极差为19 - 10 = 9(cm).
∴相同点是两段台阶路每一级台阶高度的平均数相同,不同点是两段台阶路每一级台阶高度的中位数、方差和极差均不同.
(2)甲段台阶路走起来更舒服.理由如下:
∵它的每一级台阶高度的差较小,
∴台阶高度落差不大,走起来更舒服.
(3)每一级台阶高度均修整为15cm(原数据的平均数),使得方差为0cm²,此时游客行走最方便.(答案不唯一,合理即可)
查看更多完整答案,请扫码查看


