《2025年5年中考3年模拟九年级数学全一册苏科版》

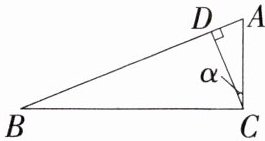
1. 「2025江苏苏州工业园星海实验中学月考」如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AB = 6$,$AC = 2$,$CD \perp AB于D$,设$\angle ACD = \alpha$,则$\cos \alpha$的值为(A)

A.$\frac{2\sqrt{2}}{3}$
B.$\frac{\sqrt{2}}{2}$
C.$2\sqrt{2}$
D.$\frac{1}{3}$

答案： A
∵∠ACB=90°,AB=6,AC=2,
∴BC=√(AB² - AC²)=4√2,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A + ∠ACD = ∠A + ∠B = 90°,
∴∠ACD = ∠B = α,
∴cos α = cos B = (BC)/(AB) = (4√2)/6 = (2√2)/3,故选A.

2. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\cos B = \frac{3}{5}$,$AB = 10\mathrm{cm}$,则$BC$的长度为6$\mathrm{cm}$。

答案： 6

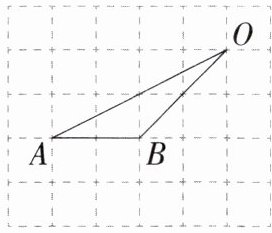
3. 「2025江苏苏州工业园金鸡湖学校月考」如图,在网格中,小正方形的边长均为$1$,点$A$、$B$、$O$都在格点上,则$\angle AOB$的正弦值是√10/10。

答案： √10/10

4. 「2025江苏扬州江都期末」已知$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\cos B = \frac{2\sqrt{2}}{3}$,则$\sin B$的值为1/3。

答案： 1/3

5. 设$\theta$为直角三角形的一个锐角,则有如下性质：①$\tan \theta = \frac{\sin \theta}{\cos \theta}$；②$\cos^{2}\theta + \sin^{2}\theta = 1$。利用这些性质解决问题。
已知$\cos \theta + \sin \theta = \frac{\sqrt{6}}{2}$,求：
(1)$\tan \theta + \frac{1}{\tan \theta}$。(2)$|\cos \theta - \sin \theta|$。

答案：
∵cos θ + sin θ = √6/2,
∴(cos θ + sin θ)² = (√6/2)²,
∴cos²θ + 2cos θ·sin θ + sin²θ = 3/2,
∴cos θ·sin θ = 1/4.
(1)tan θ +
(1)/(tan θ) = (sin θ)/(cos θ) + (cos θ)/(sin θ) = (sin²θ + cos²θ)/(cos θ·sin θ) = 1/(1/4) = 4.
(2)
∵(cos θ - sin θ)² = cos²θ - 2cos θ·sin θ + sin²θ = 1 - 2×1/4 = 1/2,
∴cos θ - sin θ = ±√2/2,
∴|cos θ - sin θ| = √2/2.

6. 「2025江西景德镇一中期中改编」三角函数$\sin 30^{\circ}$,$\cos 16^{\circ}$,$\cos 43^{\circ}$之间的大小关系是(C)
A.$\sin 30^{\circ} ＜ \cos 16^{\circ} ＜ \cos 43^{\circ}$
B.$\cos 43^{\circ} ＜ \sin 30^{\circ} ＜ \cos 16^{\circ}$
C.$\sin 30^{\circ} ＜ \cos 43^{\circ} ＜ \cos 16^{\circ}$
D.$\cos 16^{\circ} ＜ \sin 30^{\circ} ＜ \cos 43^{\circ}$

答案： C

7. 用计算器通过计算,比较下列各对数的大小,并提出你的猜想(填“＞”“＜”或“=”)。
①$\sin 30^{\circ}$=$2\sin 15^{\circ}\cos 15^{\circ}$；
②$\sin 36^{\circ}$=$2\sin 18^{\circ}\cos 18^{\circ}$；
③$\sin 45^{\circ}$=$2\sin 22.5^{\circ}\cos 22.5^{\circ}$；
④$\sin 60^{\circ}$=$2\sin 30^{\circ}\cos 30^{\circ}$；
⑤$\sin 80^{\circ}$=$2\sin 40^{\circ}\cos 40^{\circ}$。
猜想:若0° ＜ α ＜ 90°,则$\sin \alpha = 2\sin (\alpha/2)\cos (\alpha/2)$.

答案： ①=；②=；③=；④=；⑤= 猜想:若0° ＜ α ＜ 90°,则sin α = 2sin (α/2)cos (α/2).

8. 新考向数学文化「2024四川资阳中考」第14届国际数学教育大会(ICME - 14)会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”。如图2所示的“弦图”是由四个全等的直角三角形($\triangle ABE$,$\triangle BCF$,$\triangle CDG$,$\triangle DAH$)和一个小正方形$EFGH拼成的大正方形ABCD$。若$EF:AH = 1:3$,则$\sin \angle ABE = $(C)
A.$\frac{\sqrt{5}}{5}$
B.$\frac{3}{5}$
C.$\frac{4}{5}$
D.$\frac{2\sqrt{5}}{5}$

答案： C

9. 「2024江苏扬州高邮期末」如图,在$6× 6$的正方形网格中,每个小正方形的边长都是$1$,点$A$,$B$,$C$均在网格格点上,$\odot O是\triangle ABC$的外接圆,则$\cos \angle BAC$的值为(B)
A.$\frac{\sqrt{5}}{5}$
B.$\frac{2\sqrt{5}}{5}$
C.$\frac{1}{2}$
D.$\frac{\sqrt{3}}{2}$

答案： B