《2025年5年中考3年模拟九年级数学全一册苏科版》

1.「2023江苏镇江中考」如图,用一个卡钳$\left(AD= BC,\frac{OC}{OB}= \frac{OD}{OA}= \frac{1}{3}\right)测量某个零件的内孔直径AB$,量得$CD= 6cm$,则$AB= $18cm.

答案： 18

2.「2024江苏扬州广陵二模」《九章算术》中记载了一种测量井深的方法.如图所示,在井口$B处立一根垂直于井口的木杆BD$,从木杆的顶端$D观察井水水岸C$,视线$DC与井口的直径AB交于点E$,如果测得$AB= 1.8$米,$BD= 1$米,$BE= 0.5$米,那么$AC= $2.6米.

答案： 2.6

3.「2023浙江湖州中考」某数学兴趣小组测量校园内一棵树的高度,采用以下方法：如图,把支架(EF)放在离树(AB)适当距离的水平地面上的点F处,再把镜子水平放在支架(EF)上的点E处,然后沿着直线BF后退至点D处,这时恰好在镜子里看到树的顶端A,再用皮尺分别测量BF,DF,EF的长,观测者目高(CD),利用测得的数据可以求出这棵树的高度.已知$CD\perp BD$于点$D,EF\perp BD$于点$F,AB\perp BD$于点B,BF= 6米,DF= 2米,EF= 0.5米,CD= 1.7米,则这棵树的高度(AB的长)是4.1米.

答案： 4.1

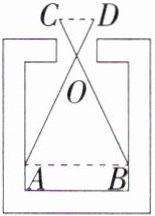
4.「2023江苏南京中考」如图,不等臂跷跷板$AB的一端A$碰到地面时,另一端$B到地面的高度为60cm$；当$AB的一端B$碰到地面时,另一端$A到地面的高度为90cm$,则跷跷板$AB的支撑点O到地面的高度OH$是(A)

A.$36cm$
B.$40cm$
C.$42cm$
D.$45cm$

答案： A

5.「2024江苏泰州兴化二模」凸透镜成像的原理如图所示,$AD// HG// BC$.若焦点$F_{1}到物体的距离与焦点F_{1}到凸透镜中心线DB的距离之比为3:1$,则物体被缩小到原来的$\frac{1}{3}$.

答案： $\frac{1}{3}$

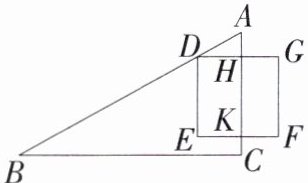
6.「2025江苏江阴文林中学月考」在《九章算术》“勾股”章中有这样一个问题：“今有邑方不知大小,各中开门,出北门二十步有木,出南门十四步,折而西行一千七百七十五步见木.问邑方几何.”大意为：如图,四边形$DEFG$是一座正方形小城,北门$H是DG$的中点,南门$K是EF$的中点,出北门$20步到A$处有一树木,出南门$14步到C$,再向西行$1775步到B$处,正好看到$A$处的树木(即点$D在直线AB$上),求小城的边长.

答案： 设小城的边长为x步,根据题意，知Rt△AHD ∽Rt△ACB,
∴$\frac{AH}{AC}=\frac{DH}{BC}$,即$\frac{20}{20 + 14 + x}=\frac{0.5x}{1775}$,整理得x² + 34x - 71000 = 0,解得x₁ = 250,x₂ = - 284(不合题意,舍去),
∴小城的边长为250步.