第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1.若关于x的方程$(m-1)x^{m^{2}+1}+mx-3= 0$是一元二次方程,则m的值是 (
A.1
B.-1
C.$\pm 1$
D.无法确定
B
)A.1
B.-1
C.$\pm 1$
D.无法确定
答案:
B
∵关于x的方程(m - 1)x^{m² + 1}+ mx - 3 = 0是一元二次方程,
∴$\left\{\begin{array}{l} m - 1≠0\\ m² + 1 = 2\end{array}\right.$,解得m = - 1。故选B。
∵关于x的方程(m - 1)x^{m² + 1}+ mx - 3 = 0是一元二次方程,
∴$\left\{\begin{array}{l} m - 1≠0\\ m² + 1 = 2\end{array}\right.$,解得m = - 1。故选B。
2.若关于x的方程$(x-4)^{2}= m+1$有实数根,则m的取值范围是 (
A.$m≥0$
B.$m≥-1$
C.$m>-1$
D.$m>1$
B
)A.$m≥0$
B.$m≥-1$
C.$m>-1$
D.$m>1$
答案:
B
∵关于x的方程(x - 4)² = m + 1有实数根,
∴m + 1≥0,解得m≥ - 1,故选B。
∵关于x的方程(x - 4)² = m + 1有实数根,
∴m + 1≥0,解得m≥ - 1,故选B。
3.「2025江苏南京玄武期中」用配方法解一元二次方程$2x^{2}-2x-1= 0$,下列配方正确的是 (
A.$(x-\frac {1}{4})^{2}= \frac {3}{4}$
B.$(x-\frac {1}{4})^{2}= \frac {3}{2}$
C.$(x-\frac {1}{2})^{2}= \frac {3}{4}$
D.$(x-\frac {1}{2})^{2}= \frac {3}{2}$
C
)A.$(x-\frac {1}{4})^{2}= \frac {3}{4}$
B.$(x-\frac {1}{4})^{2}= \frac {3}{2}$
C.$(x-\frac {1}{2})^{2}= \frac {3}{4}$
D.$(x-\frac {1}{2})^{2}= \frac {3}{2}$
答案:
C 方程2x² - 2x - 1 = 0,整理得x² - x = $\frac{1}{2}$,配方得x² - x + $\frac{1}{4}$ = $\frac{3}{4}$,即$(x - \frac{1}{2})² = \frac{3}{4}$。故选C。
4.如图,数轴上点A、B表示方程$(3x-9)^{2}-37= 0$的两个根a、b$(a>b)$,则A、B在数轴上的位置可以是 (
D
)
答案:
D
∵(3x - 9)² - 37 = 0,
∴(3x - 9)² = 37,
∴3x - 9 = ±$\sqrt{37}$,
∴x = $\frac{9 ± \sqrt{37}}{3}$,
∵a>b,
∴a = $\frac{9 + \sqrt{37}}{3}$,b = $\frac{9 - \sqrt{37}}{3}$,
∵6<$\sqrt{37}$<7,15<9 + $\sqrt{37}$<16,2<9 - $\sqrt{37}$<3,
∴5<a<$\frac{16}{3}$,$\frac{2}{3}$<b<1,故选D。
∵(3x - 9)² - 37 = 0,
∴(3x - 9)² = 37,
∴3x - 9 = ±$\sqrt{37}$,
∴x = $\frac{9 ± \sqrt{37}}{3}$,
∵a>b,
∴a = $\frac{9 + \sqrt{37}}{3}$,b = $\frac{9 - \sqrt{37}}{3}$,
∵6<$\sqrt{37}$<7,15<9 + $\sqrt{37}$<16,2<9 - $\sqrt{37}$<3,
∴5<a<$\frac{16}{3}$,$\frac{2}{3}$<b<1,故选D。
5.「2024河北中考」淇淇在计算正数a的平方时,误算成a与2的积,求得的答案比正确答案小1,则$a= $ (
A.1
B.$\sqrt {2}-1$
C.$\sqrt {2}+1$
D.1或$\sqrt {2}+1$
C
)A.1
B.$\sqrt {2}-1$
C.$\sqrt {2}+1$
D.1或$\sqrt {2}+1$
答案:
C 根据题意得a² - 2a = 1,解得a = 1 ± $\sqrt{2}$,
∵a>0,
∴a = $\sqrt{2}$ + 1。故选C。
∵a>0,
∴a = $\sqrt{2}$ + 1。故选C。
6.「2024黑龙江绥化中考」小影与小冬一起写作业,在解一道一元二次方程时,小影在化简过程中写错了常数项,因而得到方程的两个根是6和1;小冬在化简过程中写错了一次项的系数,因而得到方程的两个根是-2和-5.则原来的方程是 (
A.$x^{2}+6x+5= 0$
B.$x^{2}-7x+10= 0$
C.$x^{2}-5x+2= 0$
D.$x^{2}-6x-10= 0$
B
)A.$x^{2}+6x+5= 0$
B.$x^{2}-7x+10= 0$
C.$x^{2}-5x+2= 0$
D.$x^{2}-6x-10= 0$
答案:
B 设原来的方程为ax² + bx + c = 0(a≠0),由题意知, - $\frac{b}{a}$ = 6 + 1 = 7,$\frac{c}{a}$ = - 2×( - 5) = 10,所以b = - 7a,c = 10a,所以原来的方程为ax² - 7ax + 10a = 0,因为a≠0,所以x² - 7x + 10 = 0。故选B。
7.「2025江苏无锡梁溪江南中学月考」已知一元二次方程$ax^{2}+bx+c= 0(a≠0)$,下列说法:①若$x= 0$是方程的一个根,则$c= 0$;②若$a-b+c= 0且4a+2b+c= 0$,则$x_{1}+x_{2}= 1,x_{1}x_{2}= -2$;③若方程$a(x-1)^{2}+b(x-1)+c= 0存在两个根x_{1}= 2,x_{2}= 5$,则方程$ax^{2}+bx+c= 0的两个根为x_{1}= 1,x_{2}= 4$;④若c是方程$ax^{2}+bx+c= 0$的一个根,则一定有$ac+b+1= 0$成立.其中一定正确的是 (
A.①②④
B.①③④
C.①②③
D.①②③④
C
)A.①②④
B.①③④
C.①②③
D.①②③④
答案:
C ①把x = 0代入ax² + bx + c = 0,得c = 0,故①符合题意;②
∵a - b + c = 0且4a + 2b + c = 0,
∴方程的两个根为x₁ = - 1,x₂ = 2,
∴x₁ + x₂ = 1,x₁x₂ = - 2,故②符合题意;③
∵方程a(x - 1)² + b(x - 1) + c = 0存在两个根x₁ = 2,x₂ = 5,
∴x - 1 = 1或x - 1 = 4,
∴方程ax² + bx + c = 0的两个根为x₁ = 1,x₂ = 4,故③符合题意;④
∵c是方程ax² + bx + c = 0的一个根,
∴ac² + bc + c = 0,即c(ac + b + 1) = 0,
∴c = 0或ac + b + 1 = 0,故④不符合题意。综上所述,一定正确的是①②③,故选C。
∵a - b + c = 0且4a + 2b + c = 0,
∴方程的两个根为x₁ = - 1,x₂ = 2,
∴x₁ + x₂ = 1,x₁x₂ = - 2,故②符合题意;③
∵方程a(x - 1)² + b(x - 1) + c = 0存在两个根x₁ = 2,x₂ = 5,
∴x - 1 = 1或x - 1 = 4,
∴方程ax² + bx + c = 0的两个根为x₁ = 1,x₂ = 4,故③符合题意;④
∵c是方程ax² + bx + c = 0的一个根,
∴ac² + bc + c = 0,即c(ac + b + 1) = 0,
∴c = 0或ac + b + 1 = 0,故④不符合题意。综上所述,一定正确的是①②③,故选C。
8.欧几里得的《几何原本》中记载,方程$x^{2}+ax= b^{2}$的图解法是:画$Rt△ABC$,使$∠ACB= 90^{\circ },BC= \frac {a}{2},AC= b$,再在斜边AB上截取$BD= BC$,则该方程的一个正根是 (
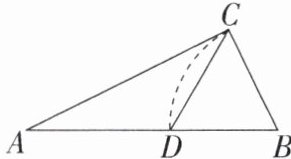
A.AC的长
B.CD的长
C.AD的长
D.BC的长
C
)
A.AC的长
B.CD的长
C.AD的长
D.BC的长
答案:
C 【解法一】在Rt△ABC中,由勾股定理可得AC² + BC² = AB²。
∵AC = b,BD = BC = $\frac{a}{2}$,
∴b² + ($\frac{a}{2}$)² = $(AD + \frac{a}{2})²$ = AD² + aAD + ($\frac{a}{2}$)²,
∴AD² + aAD = b²,
∴AD的长是方程x² + ax = b²的一个正根。故选C。
【解法二】原方程可变形为x² + ax - b² = 0,
∴根的判别式 = a² + 4b²>0,
∴x = $\frac{- a ± \sqrt{a² + 4b²}}{2}$,其中正根为x = $\frac{- a + \sqrt{a² + 4b²}}{2}$。
∵BC² + AC² = AB²,即$\frac{a²}{4}$ + b² = AB²,
∴a² + 4b² = 4AB²,
∴x = $\frac{- a + \sqrt{a² + 4b²}}{2}$ = $\frac{- a + 2AB}{2}$ = AB - $\frac{a}{2}$ = AB - BD = AD,
∴AD的长是方程x² + ax = b²的一个正根。故选C。
∵AC = b,BD = BC = $\frac{a}{2}$,
∴b² + ($\frac{a}{2}$)² = $(AD + \frac{a}{2})²$ = AD² + aAD + ($\frac{a}{2}$)²,
∴AD² + aAD = b²,
∴AD的长是方程x² + ax = b²的一个正根。故选C。
【解法二】原方程可变形为x² + ax - b² = 0,
∴根的判别式 = a² + 4b²>0,
∴x = $\frac{- a ± \sqrt{a² + 4b²}}{2}$,其中正根为x = $\frac{- a + \sqrt{a² + 4b²}}{2}$。
∵BC² + AC² = AB²,即$\frac{a²}{4}$ + b² = AB²,
∴a² + 4b² = 4AB²,
∴x = $\frac{- a + \sqrt{a² + 4b²}}{2}$ = $\frac{- a + 2AB}{2}$ = AB - $\frac{a}{2}$ = AB - BD = AD,
∴AD的长是方程x² + ax = b²的一个正根。故选C。
9.「2025江苏连云港东海月考」求方程$x^{2}+3x+2= 0$的根时,根据求根公式,列式为$x= \frac {m\pm \sqrt {9-4×1×2}}{2×1}$,则m的值为
-3
.
答案:
答案 - 3
解析 根据题意可得x = $\frac{- 3 ± \sqrt{9 - 4×1×2}}{2×1}$,故m = - 3。
解析 根据题意可得x = $\frac{- 3 ± \sqrt{9 - 4×1×2}}{2×1}$,故m = - 3。
10.若a是关于x的方程$3x^{2}-x-1= 0$的一个根,则2024-$6a^{2}+2a$的值是
2022
.
答案:
答案 2022
解析
∵a是关于x的方程3x² - x - 1 = 0的一个根,
∴3a² - a - 1 = 0,即3a² - a = 1,
∴2024 - 6a² + 2a = 2024 - 2(3a² - a) = 2024 - 2×1 = 2022。
解析
∵a是关于x的方程3x² - x - 1 = 0的一个根,
∴3a² - a - 1 = 0,即3a² - a = 1,
∴2024 - 6a² + 2a = 2024 - 2(3a² - a) = 2024 - 2×1 = 2022。
查看更多完整答案,请扫码查看


