第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
12.「2025江苏无锡江阴青阳初中月考节选」说明代数式:$2x^{2}+8x+y^{2}-8y+25$的值一定是一个正数。
答案:
证明
∵2x²+8x+y²-8y+25=2(x²+4x+4)+y²-8y+16+1=2(x+2)²+(y-4)²+1,
∴2(x+2)²+(y-4)²+1≥1,
∴2x²+8x+y²-8y+25的值一定为正数.
∵2x²+8x+y²-8y+25=2(x²+4x+4)+y²-8y+16+1=2(x+2)²+(y-4)²+1,
∴2(x+2)²+(y-4)²+1≥1,
∴2x²+8x+y²-8y+25的值一定为正数.
13.「2025江苏泰州靖江靖城中学月考」“配方法”在数学中非常有用.有时我们可以将代数式配成完全平方式,如:$x^{2}+4x+5= x^{2}+4x+4+1= (x+2)^{2}+1,\because (x+2)^{2}≥0,\therefore (x+2)^{2}+1≥1,\therefore x^{2}+4x+5≥1$。有时我们也可以用配方法解一元二次方程.请利用“配方法”解决问题:
(1)当$x=$
(2)如图,在矩形ABCD中,$AB= a(a<2),BC= 2$。以点D为圆心,CD的长为半径画弧,交AD于点E,交BD于点F.请指出图中哪条线段的长是方程$x^{2}+2ax= 4$的一个根,并说明理由。
]
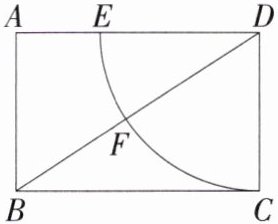
线段BF的长是方程x²+2ax=4的一个根.理由如下:
∵矩形ABCD中,AB=a(a<2),BC=2,
∴AD=BC=2,CD=AB=a,∠A=90°,
∴BD=√(a²+2²)=√(a²+4),由作图可知,DF=DC=a,
∴BF=BD-DF=√(a²+4)-a,
∵x²+2ax=4,
∴x²+2ax+a²=4+a²,
∴(x+a)²=4+a²,
∴x+a=±√(4+a²),
∴x₁=√(4+a²)-a,x₂=-√(4+a²)-a,
∴线段BF的长为方程x²+2ax=4的一个根.
(1)当$x=$
2
时,代数式$x^{2}-4x+7$有最小
(填“大”或“小”)值,这个最值为3
。(2)如图,在矩形ABCD中,$AB= a(a<2),BC= 2$。以点D为圆心,CD的长为半径画弧,交AD于点E,交BD于点F.请指出图中哪条线段的长是方程$x^{2}+2ax= 4$的一个根,并说明理由。
]

线段BF的长是方程x²+2ax=4的一个根.理由如下:
∵矩形ABCD中,AB=a(a<2),BC=2,
∴AD=BC=2,CD=AB=a,∠A=90°,
∴BD=√(a²+2²)=√(a²+4),由作图可知,DF=DC=a,
∴BF=BD-DF=√(a²+4)-a,
∵x²+2ax=4,
∴x²+2ax+a²=4+a²,
∴(x+a)²=4+a²,
∴x+a=±√(4+a²),
∴x₁=√(4+a²)-a,x₂=-√(4+a²)-a,
∴线段BF的长为方程x²+2ax=4的一个根.
答案:
(1)2;小;3
(2)线段BF的长是方程x²+2ax=4的一个根.理由如下:
∵矩形ABCD中,AB=a(a<2),BC=2,
∴AD=BC=2,CD=AB=a,∠A=90°,
∴BD=√(a²+2²)=√(a²+4),由作图可知,DF=DC=a,
∴BF=BD-DF=√(a²+4)-a,
∵x²+2ax=4,
∴x²+2ax+a²=4+a²,
∴(x+a)²=4+a²,
∴x+a=±√(4+a²),
∴x₁=√(4+a²)-a,x₂=-√(4+a²)-a,
∴线段BF的长为方程x²+2ax=4的一个根.
(1)2;小;3
(2)线段BF的长是方程x²+2ax=4的一个根.理由如下:
∵矩形ABCD中,AB=a(a<2),BC=2,
∴AD=BC=2,CD=AB=a,∠A=90°,
∴BD=√(a²+2²)=√(a²+4),由作图可知,DF=DC=a,
∴BF=BD-DF=√(a²+4)-a,
∵x²+2ax=4,
∴x²+2ax+a²=4+a²,
∴(x+a)²=4+a²,
∴x+a=±√(4+a²),
∴x₁=√(4+a²)-a,x₂=-√(4+a²)-a,
∴线段BF的长为方程x²+2ax=4的一个根.
例题 已知$P= \frac {7}{15}m-1,Q= m^{2}-\frac {8}{15}m$(m为任意实数),比较大小:P
<
Q。(填“>”“<”或“=”)
答案:
<
变式1【二次项系数不为1】「2023江苏无锡江南大学附中二模」已知$M= 2x^{2}-2x+3,N= 4x^{2}-3x+4$,请比较M和N的大小。
答案:
∵M=2x²-2x+3,N=4x²-3x+4,
∴M-N=(2x²-2x+3)-(4x²-3x+4)=2x²-2x+3-4x²+3x-4=-2x²+x-1=-2(x-1/4)²-7/8<0,
∴M<N.
∵M=2x²-2x+3,N=4x²-3x+4,
∴M-N=(2x²-2x+3)-(4x²-3x+4)=2x²-2x+3-4x²+3x-4=-2x²+x-1=-2(x-1/4)²-7/8<0,
∴M<N.
变式2【单字母改为双字母】「2024北京十五中期中」试判断代数式$a^{2}+2b^{2}+11与2ab+2a+4b$的大小,并说明理由。
答案:
a²+2b²+11>2ab+2a+4b.理由如下:
∵(a²+2b²+11)-(2ab+2a+4b)=a²+2b²+11-2ab-2a-4b=[(a²-2ab+b²)+(-2a+2b)+1]+(b²-6b+9)+1=[(a-b)²-2(a-b)+1]+(b-3)²+1=(a-b-1)²+(b-3)²+1>0,
∴a²+2b²+11>2ab+2a+4b.
∵(a²+2b²+11)-(2ab+2a+4b)=a²+2b²+11-2ab-2a-4b=[(a²-2ab+b²)+(-2a+2b)+1]+(b²-6b+9)+1=[(a-b)²-2(a-b)+1]+(b-3)²+1=(a-b-1)²+(b-3)²+1>0,
∴a²+2b²+11>2ab+2a+4b.
查看更多完整答案,请扫码查看


