《2025年5年中考3年模拟九年级数学全一册苏科版》

1.跨自由落体运动 [2024天津中考]从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是$h = 30t - 5t^{2}(0≤t≤6)$.有下列结论:①小球从抛出到落地需要6s;②小球运动中的高度可以是30m;③小球运动2s时的高度小于运动5s时的高度.其中,正确的个数是(C)
A.0
B.1
C.2
D.3

答案： C　①令h=0,则30t−5t²=0,解得t₁=0,t₂=6,
∴小球从抛出到落地需要6s,故①正确;②h=30t−5t²=−5(t²−6t)=−5(t−3)²+45,
∵−5＜0,
∴当t=3时,h有最大值，最大值为45,
∴小球运动中的高度可以是30m,故②正确;③t=2时,h=30×2−5×4=40,t=5时,h=30×5−5×25=25,
∴小球运动2s时的高度大于运动5s时的高度,故③错误.故选C.

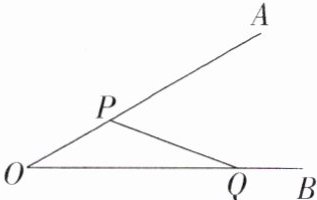
2.如图,要在夹角为$30^{\circ}$的两条小路OA与OB形成的角状空地上建一个三角形花坛,分别在边OA和OB上取点P和点Q,并扎起篱笆将花坛保护起来(篱笆的厚度忽略不计).若OP和OQ两段篱笆的总长为60m,则该花坛($△POQ$)面积的最大值为____$m^{2}$.

答案：
答案225
解析　如图,过P作PC⊥OB于点C,设OP的长为xm,

△POQ的面积为Sm²,则OQ的长为(60−x)m,
∵∠POQ=30°,
∴PC=$\frac{1}{2}$OP=$\frac{1}{2}$x(m),
∴S=$\frac{1}{2}$×$\frac{1}{2}$x·(60−x)=−$\frac{1}{4}$(x−30)²+225(0＜x＜60),
∴当x=30时,S取得最大值,为225,即当OP的长为30m时，△POQ的面积最大，最大值为225m².

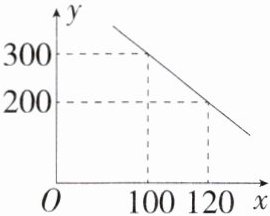
3.[2024山东济宁中考]某商场以每件80元的价格购进一种商品,在一段时间内,销售量y(单位:件)与销售单价x(单位:元)之间是一次函数关系,其部分图像如图所示.
(1)求这段时间内y与x之间的函数解析式.
(2)在这段时间内,若销售单价不低于100元,且商场还要完成不少于220件的销售任务,当销售单价为多少时,商场获得最大利润?最大利润是多少?

答案： 解析　
(1)设一次函数的解析式为y=kx+b,把(100,300),(120,200)代入,得$\begin{cases}100k + b = 300\\120k + b = 200\end{cases}$，解得$\begin{cases}k = -5\\b = 800\end{cases}$，
∴所求函数解析式为y=−5x+800.
(2)由题意得，$\begin{cases}x \geq 100\\-5x + 800 \geq 220\end{cases}$，
∴100≤x≤116.
∵商场获得的利润=(x−80)(−5x+800)=−5x²+1200x−64000=−5(x−120)²+8000,又−5＜0,100≤x≤116,
∴当x=116时,获得的利润最大，最大值为7920.
答:当销售单价为116时，商场获得最大利润，最大利润是7920元。

4.[2025江苏苏州姑苏期中]汽车刹车后行驶的距离s(单位:米)关于行驶时间t(单位:秒)的函数关系式是$s = 6t - t^{2}$,则汽车从刹车到停止所用时间为(B)
A.4秒
B.3秒
C.2秒
D.1秒

答案： B
∵s=6t−t²=−(t−3)²+9,
∴当t=3时,s取得最大值,即汽车停下来，故选B.

5.[2024四川自贡中考]九(1)班劳动实践基地内有一块面积足够大的平整空地,地上两段围墙$AB⊥CD$于点O(如图),其中AB上的EO段围墙空缺.同学们测得$AE = 6.6m,OE = 1.4m,OB = 6m,OC = 5m,OD = 3m$,班长买来可切断的围栏16m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是____46.4$m^{2}$.

答案： 答案46.4
解析　设所围矩形在射线OA上的一段长为xm,菜地的面积为Sm².
(1)当x≤8时,S=x·$\frac{16−x−1.4 + 5}{2}$=−$\frac{1}{2}$x²+9.8x=−$\frac{1}{2}$(x−9.8)²+48.02,当x=8时,S最大,为46.4;
(2)当x＞8时,S=x·$\frac{16 + 6.6 + 5}{2}$−x=−x²+13.8x=−(x−6.9)²+47.61,在x＞8的范围内,S均小于46.4.所以该菜地的最大面积为46.4m².

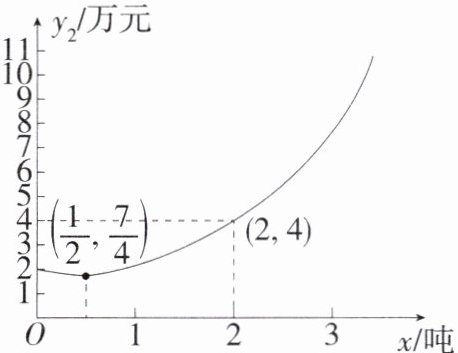
6.[2024新疆生产建设兵团中考]某公司销售一批产品,经市场调研发现,当销售量在0.4吨和3.5吨之间时,销售额$y_{1}$(万元)与销售量x(吨)的函数解析式为$y_{1} = 5x$;成本$y_{2}$(万元)与销售量x(吨)的函数图像是如图所示的抛物线的一部分,其中$(\frac{1}{2},\frac{7}{4})$是其顶点.

(1)求出成本$y_{2}$关于销售量x的函数解析式.
(2)当成本最低时,销售产品所获利润是多少?
(3)当销售量是多少吨时,可获得最大利润?最大利润是多少?
(注:利润= 销售额-成本)

答案： 解析　
(1)
∵顶点为($\frac{1}{2}$,$\frac{7}{4}$)，
∴可设抛物线解析式为y₂=a(x−$\frac{1}{2}$)²+$\frac{7}{4}$.又抛物线过(2,4),
∴a×$\frac{9}{4}$+$\frac{7}{4}$=4，
∴a=1.
∴y₂=(x−$\frac{1}{2}$)²+$\frac{7}{4}$.
(2)由题意得,当销售量x=$\frac{1}{2}$时，成本最低，为$\frac{7}{4}$,又销售量在0.4吨和3.5吨之间时，销售额y₁(万元)与销售量x(吨)の函数解析式为y₁=5x,
∴当x=$\frac{1}{2}$时,销售额y₁=5x=5×$\frac{1}{2}$=2.5.
∴此时利润为2.5−$\frac{7}{4}$=0.75(万元).
答:当成本最低时，销售产品所获利润是0.75万元.
(3)由题意得,利润=y₁−y₂=5x−[(x−$\frac{1}{2}$)²+$\frac{7}{4}$]=−x²+6x−2=−(x−3)²+7.
∵−1＜0,
∴当x=3时,利润取最大值，最大值为7.
答:当销售量是3吨时，可获得最大利润，最大利润是7万元。