第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1.新数学文化「2025江苏南京鼓楼期中」战国时期的著作《墨经》中……“,一中同长也”描述的图形是(
A.等边三角形
B.正方形
C.正六边形
D.圆
D
)A.等边三角形
B.正方形
C.正六边形
D.圆
答案:
D “一中同长也”表示圆心到圆上各点的距离都相等,即半径都相等.故选D.
2.「2025江苏南京金陵中学河西分校期中」下列说法:①同一圆上的点到圆心的距离相等;②若某几个点到一个定点的距离相等,则这几个点共圆;③半径确定了,圆就确定了.其中正确的是(
A.①②
B.①③
C.②③
D.①②③
A
)A.①②
B.①③
C.②③
D.①②③
答案:
A ①同一圆上的点到圆心的距离都等于该圆的半径,故①正确;②到定点距离等于定长的点都在以定点为圆心,定长为半径的圆上,故②正确;③半径确定了,圆的大小确定了,但是圆的位置不能确定,故③不正确.综上所述,正确的是①②,故选A.
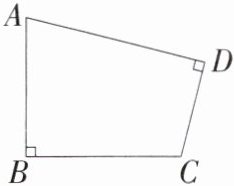
3.「2025江苏南京迈皋桥初级中学月考」如图所示,在四边形ABCD中,∠B= ∠D= 90°,求证:A、B、C、D四点在同一个圆上.

答案:
证明 连接AC,取AC的中点O,连接OB,OD,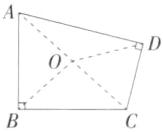
∵∠ABC=∠ADC=90°,
∴OB=$\frac{1}{2}$AC,OD=$\frac{1}{2}$AC,
∴OB=OA=OC=OD,
∴A、B、C、D四点在同一个圆上.
证明 连接AC,取AC的中点O,连接OB,OD,

∵∠ABC=∠ADC=90°,
∴OB=$\frac{1}{2}$AC,OD=$\frac{1}{2}$AC,
∴OB=OA=OC=OD,
∴A、B、C、D四点在同一个圆上.
4.「2025江苏无锡滨湖期中」已知⊙O的直径为10cm,若线段OA的长为6cm,则点A与⊙O的位置关系是(
A.点A在⊙O上
B.点A在⊙O外
C.点A在⊙O内
D.无法确定
B
)A.点A在⊙O上
B.点A在⊙O外
C.点A在⊙O内
D.无法确定
答案:
B
∵⊙O的直径为10cm,
∴⊙O的半径为5cm,
∵OA=6cm>5cm,
∴点A在⊙O外.故选B
∵⊙O的直径为10cm,
∴⊙O的半径为5cm,
∵OA=6cm>5cm,
∴点A在⊙O外.故选B
5.「2025江苏扬州高邮城北中学月考」在Rt△ABC中,∠C= 90°,BC= 5,AC= 12,以点B为圆心,12为半径画圆,则点A与⊙B的位置关系是(
A.点A在⊙B外
B.点A在⊙B上
C.点A在⊙B内
D.无法确定
A
)A.点A在⊙B外
B.点A在⊙B上
C.点A在⊙B内
D.无法确定
答案:
A 由题意可得AB=$\sqrt{BC^2+AC^2}$=$\sqrt{5^2+12^2}$=13.
∵AB=13>12,
∴点A在⊙B外,故选A.
∵AB=13>12,
∴点A在⊙B外,故选A.
6.如图,已知矩形ABCD的边AB= 6,BC= 8,现以点A为圆心作圆,如果B、C、D至少有一点在圆内,且至少有一点在圆外,那么⊙A的半径r的取值范围是______.


答案:
6<r<10 解析 如图,连接AC,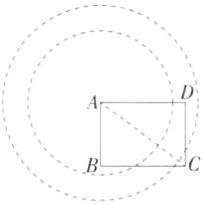
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AC=$\sqrt{AB^2+BC^2}$=$\sqrt{6^2+8^2}$=10.
∵以点A为圆心作圆,B、C、D至少有一点在圆内,
∴r>6,
∵B、C、D至少有一点在圆外,
∴r<10,
∴⊙A的半径r的取值范围是6<r<10.
6<r<10 解析 如图,连接AC,

∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AC=$\sqrt{AB^2+BC^2}$=$\sqrt{6^2+8^2}$=10.
∵以点A为圆心作圆,B、C、D至少有一点在圆内,
∴r>6,
∵B、C、D至少有一点在圆外,
∴r<10,
∴⊙A的半径r的取值范围是6<r<10.
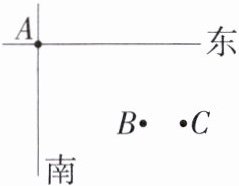
7.「2025江苏连云港灌云月考」如图,点A表示一座风景秀美的小山,市政府计划以点A为中心,修建一个半径为12km的“桃园山庄”.因此,在此范围内的其他建筑物将被拆除.从点A出发向东走8km,再向南走6km有一砖厂B,砖厂B的正东方向3km处有一古塔C,问砖厂和古塔是否需要拆除?

答案:
解析 以正东、正北方向分别为x轴、y轴的正方向,建立平面直角坐标系,连接AB,AC(图略),过点B,C 分别作x轴、y轴的垂线,则AB=$\sqrt{8^2+6^2}$=10(km),AC=$\sqrt{(8+3)^2+6^2}$=$\sqrt{157}$(km),
∵10<12,
∴砖厂需要拆除,
∵$\sqrt{157}$>12,
∴古塔不需要拆除.
∵10<12,
∴砖厂需要拆除,
∵$\sqrt{157}$>12,
∴古塔不需要拆除.
查看更多完整答案,请扫码查看


