《2025年5年中考3年模拟九年级数学全一册苏科版》

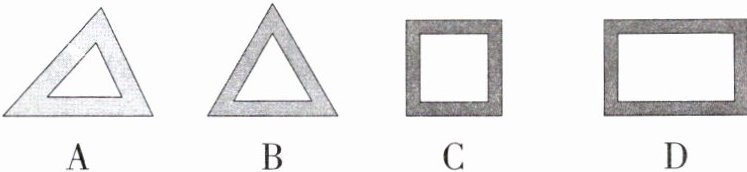
8. 「2025江苏靖江八校联考,☆☆」手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所成的几何图形不一定相似的是(D)

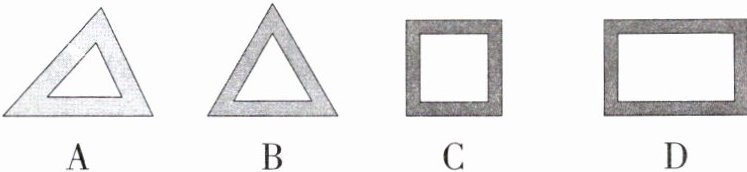
答案： D 设D中大矩形的长与宽分别为A,B,花边宽度为x,则小矩形的长与宽分别为a - 2x,b - 2x,$\frac{a}{b}$和$\frac{a - 2x}{b - 2x}$不一定相等,故选 D.

9. 「☆☆」已知两个直角三角形的三边长分别为3,4,m和6,8,n,且这两个直角三角形不相似,则m+n的值为$( )$A

答案： A 当3,4为直角边长,6,8也为直角边长时,两三角形相似,不合题意;当三边长分别为3,4,$\sqrt{7}$和6,8,$2\sqrt{7}$时,两三角形相似,不合题意;当3,4为直角边长时,m=5,则8为另一直角三角形的斜边长,
∴n=$\sqrt{8^2 - 6^2}=2\sqrt{7}$,
∴m + n=5 + $2\sqrt{7}$;当6,8为直角边长时,n=10,则4为另一直角三角形的斜边长,
∴m=$\sqrt{4^2 - 3^2}=\sqrt{7}$,
∴m + n=10 + $\sqrt{7}$.综上,m + n=5 + $2\sqrt{7}$或10 + $\sqrt{7}$.故选 A.

10. 「2024河南洛阳洛龙模拟,☆☆」如图,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD相似,且对应边之比为$\frac{\sqrt{5}}{3},则\frac{AE},{BE}(AE＜BE)$的值为______。
]

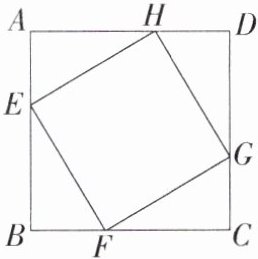
$\frac{1}{2}$

答案： 答案 $\frac{1}{2}$解析
∵正方形EFGH与正方形ABCD相似,且对应边之比为$\frac{\sqrt{5}}{3}$,
∴$\frac{EF}{AB}=\frac{\sqrt{5}}{3}$,设EF=$\sqrt{5}k$,AB=3k(k ＞ 0),
∵∠B=∠FEH=90°,
∴∠AEH+∠BEF=90°,∠BEF+∠EFB=90°,
∴∠AEH=∠EFB,又
∵EH=EF,∠A=∠B=90°,
∴△HAE≌△EBF,
∴AE=BF,设AE=BF=x,则EB=3k - x,在Rt△EFB中,
∵$EF^2=BE^2+BF^2$,
∴$(\sqrt{5}k)^2=(3k - x)^2+x^2$,整理得$x^2 - 3kx + 2k^2=0$,解得x₁=k,x₂=2k(舍去),
∴AE=k,BE=2k,
∴$\frac{AE}{BE}=\frac{1}{2}$.

11. 新考向新定义题「2025上海静安市西初中段考,☆☆」如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中,$AB= AC= \sqrt{3},$$AD= CD= \frac{3},{2},$点E,点F分别是边AD,边BC的中点。如果AC是凸四边形ABCD的相似对角线,那么EF的长为______。

答案：
答案 $\frac{\sqrt{41}}{4}$解析 如图所示:
∵AB=AC,AD=CD,△ABC∽△DAC,
∴$\frac{AB}{AD}=\frac{BC}{AC}$,即$\frac{AC}{AD}=\frac{BC}{AC}$,
∴$AC^2=BC·AD$,
∵AC=$\sqrt{3}$,AD=$\frac{3}{2}$,
∴BC=2,
∵△ABC∽△DAC,
∴∠ACB=∠ACD=∠CAD,
∴BC//AD,
∵AB=AC,F为BC的中点,
∴AF⊥BC,BF=CF=1,
∴∠AFC=90°,
∵BC//AD,
∴∠FAE=180° - 90°=90°,在Rt△AFC中,
∵AC=$\sqrt{3}$,FC=1,
∴AF=$\sqrt{2}$,
∵AD=$\frac{3}{2}$,E为AD的中点,
∴AE=$\frac{3}{4}$,
∴EF=$\sqrt{AF^2+AE^2}=\sqrt{(\sqrt{2})^2+(\frac{3}{4})^2}=\frac{\sqrt{41}}{4}$.

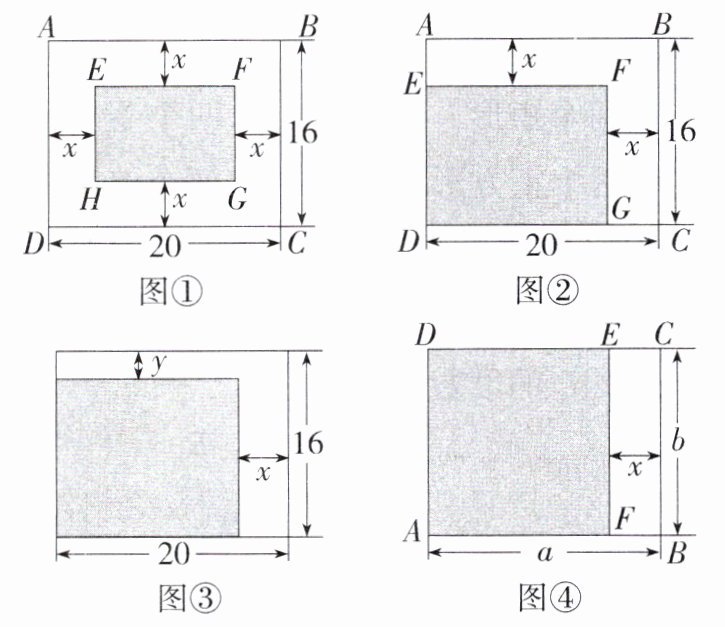
12. 新课标推理能力新课标模型观念某矩形场地长20m,宽16m。
(1) 如图①,在场地中央建有一矩形草坪,沿草坪四周外围有x m宽的小路,小路内外边缘所成的矩形相似吗？
(2) 如果矩形场地中矩形草坪的变化如图②所示,两个矩形相似吗？
(3) 如果变化如图③所示,它们能相似吗？若能相似,求x,y满足的关系式。
(4) 如果变化如图④所示,矩形ABCD与矩形ADEF能否相似？若能相似,求x的值(其中a＞b)。

答案： 解析
(1)
∵AB=CD=20 m,AD=BC=16 m,EF=GH=(20 - 2x)m,EH=FG=(16 - 2x)m,
∴$\frac{EF}{AB}=\frac{20 - 2x}{20}=1-\frac{x}{10}$,$\frac{EH}{AD}=\frac{16 - 2x}{16}=1-\frac{x}{8}$.
∵$1-\frac{x}{10}≠1-\frac{x}{8}$,
∴$\frac{EF}{AB}≠\frac{EH}{AD}$.
∴小路内外边缘所成的矩形不相似.
(2)
∵20＞16,
∴20 - x＞16 - x,
∴EF＞FG.如果两个矩形相似,那么有$\frac{EF}{AB}=\frac{FG}{BC}$,即$\frac{20 - x}{20}=\frac{16 - x}{16}$,解得x=0,不符合题意,
∴两个矩形不相似.
(3)能.当$\frac{20 - x}{20}=\frac{16 - y}{16}$时,x=$\frac{5}{4}y$(0＜y＜16).当$\frac{20 - x}{16}=\frac{16 - y}{20}$时,y=$\frac{5}{4}x$-9(7.2＜x＜20).
∴当x=$\frac{5}{4}y$(0＜y＜16)或y=$\frac{5}{4}x$-9(7.2＜x＜20)时,两个矩形相似.
(4)能.假设矩形ABCD与矩形ADEF相似,则$\frac{DE}{BC}=\frac{AD}{AB}$,即$\frac{a - x}{b}=\frac{b}{a}$,解得x=$\frac{a^2 - b^2}{a}$.
∴矩形ABCD与矩形ADEF能相似,此时x=$\frac{a^2 - b^2}{a}$.