《2025年5年中考3年模拟九年级数学全一册苏科版》

9. 「2024 山东日照中考,☆☆」如图,在菱形 $ABCD$ 中,$AB = 2$,$\angle B = 120^{\circ}$,点 $O$ 是对角线 $AC$ 的中点,以点 $O$ 为圆心,$OA$ 长为半径作圆心角为 $60^{\circ}$ 的扇形 $OEF$,点 $D$ 在扇形 $EOF$ 内,则图中阴影部分的面积为(A)

A.$\frac{\pi}{2}-\frac{\sqrt{3}}{4}$
B.$\pi-\frac{\sqrt{3}}{4}$
C.$\frac{\pi}{2}-\frac{1}{4}$
D.无法确定

答案： A

10. 「2023 内蒙古通辽中考,☆☆」如图,在扇形 $AOB$ 中,$\angle AOB = 60^{\circ}$,$OD$ 平分 $\angle AOB$ 交 $\overset{\frown}{AB}$ 于点 $D$,点 $C$ 是半径 $OB$ 上一动点,若 $OA = 1$,则阴影部分周长的最小值为(A)
A.$\sqrt{2}+\frac{\pi}{6}$
B.$\sqrt{2}+\frac{\pi}{3}$
C.$2\sqrt{2}+\frac{\pi}{6}$
D.$2\sqrt{2}+\frac{\pi}{3}$

答案： A

11. 「2025 江苏南京建邺期末,☆☆」如图,$\odot O$ 经过 $AO$ 的中点 $B$,$OB = 1$,点 $P$ 为 $\odot O$ 上一动点,过点 $B$ 作 $AP$ 的垂线,垂足为 $Q$。当点 $P$ 旋转一周时,点 $Q$ 运动的路程为$\frac{2\pi}{3}$。

答案： $\frac{2\pi}{3}$

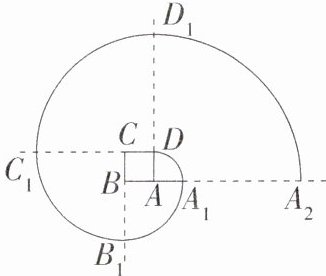
12. 「2022 四川广安中考,☆☆」如图,四边形 $ABCD$ 是边长为 $\frac{1}{2}$ 的正方形,曲线 $DA_{1}B_{1}C_{1}D_{1}A_{2}…$ 是由多段 $90^{\circ}$ 的圆心角所对的弧组成的,其中,弧 $DA_{1}$ 的圆心为 $A$,半径为 $AD$；弧 $A_{1}B_{1}$ 的圆心为 $B$,半径为 $BA_{1}$；弧 $B_{1}C_{1}$ 的圆心为 $C$,半径为 $CB_{1}$；弧 $C_{1}D_{1}$ 的圆心为 $D$,半径为 $DC_{1}$；……弧 $DA_{1}$、弧 $A_{1}B_{1}$、弧 $B_{1}C_{1}$、弧 $C_{1}D_{1}$、……的圆心依次按点 $A$、$B$、$C$、$D$ 循环,则弧 $C_{2022}D_{2022}$ 的长是2022π(结果保留 $\pi$)。

答案： 2022π

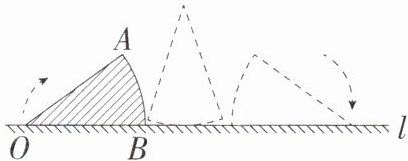
13. 新课标 几何直观 (1)如图,将含 $30^{\circ}$ 角的三角尺 $ABC$ 的斜边放置在直线 $l$ 上,并按顺时针方向在直线 $l$ 上无滑动翻动两次,使它翻到 $\triangle A''B''C''$ 的位置上,设斜边 $AB = 2$,则点 $A$ 运动到点 $A''$ 的位置时,点 $A$ 经过的路线长为$\frac{4\pi}{3}+\frac{\sqrt{3}}{2}\pi$,点 $A$ 经过的路线与直线 $l$ 所围成的面积为$\frac{25}{12}\pi+\frac{\sqrt{3}}{2}$。


(2)「2024 江苏宿迁沭阳调研」如图,在扇形纸片 $AOB$ 中,$OA = 10$,$\angle AOB = 36^{\circ}$,$OB$ 在桌面内的直线 $l$ 上。现将此扇形沿 $l$ 按顺时针方向旋转(旋转过程中无滑动),当 $OA$ 落在 $l$ 上时,停止旋转,则点 $O$ 所经过的路线长为12π。

答案：
(1)$\frac{4\pi}{3}+\frac{\sqrt{3}}{2}\pi$；$\frac{25}{12}\pi+\frac{\sqrt{3}}{2}$
(2)12π