第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
8.新分类讨论思想「2024江苏扬州广陵月考,★☆」在同一平面内,点P到圆上的点的最大距离为6,最小距离为4,则此圆的半径为(
A.2
B.5
C.1
D.5或1
D
)A.2
B.5
C.1
D.5或1
答案:
D 设圆的半径为r,当点P在圆外时,r=$\frac{6−4}{2}$=1;当点P在圆内时,r=$\frac{6+4}{2}$=5. 综上,圆的半径为1或5.故选D.
9.「2024浙江金华东阳期末,★☆」在等腰三角形ABC中,AB= AC,点D是AC的中点,若以AB为直径作⊙O,则下列判断正确的是( )
A.点C一定在⊙O外
B.点C一定在⊙O上
C.点D一定在⊙O外
D.点D一定在⊙O上
A.点C一定在⊙O外
B.点C一定在⊙O上
C.点D一定在⊙O外
D.点D一定在⊙O上
答案:
A 因为AB为⊙O的直径,直径为最长的弦,AB=AC,所以点C一定在⊙O外,如图①②③,点D的情况有三种,点D可能在⊙O内,可能在⊙O上,也可能在⊙O外.故选A.


A 因为AB为⊙O的直径,直径为最长的弦,AB=AC,所以点C一定在⊙O外,如图①②③,点D的情况有三种,点D可能在⊙O内,可能在⊙O上,也可能在⊙O外.故选A.



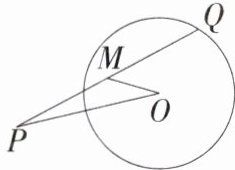
10.「2025江苏苏州五校联考期中,★☆」如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM,若⊙O的半径为4,OP= 8,则线段OM长的最小值是( )
A.2
B.3
C.4
D.5

A.2
B.3
C.4
D.5
答案:
A 设OP与⊙O交于点N,连接MN,OQ,如图.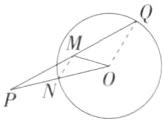
∵OP=8,ON=4,
∴N是OP的中点.又
∵M是PQ的中点,
∴MN为△POQ的中位线,
∴MN=$\frac{1}{2}$OQ=$\frac{1}{2}$× 4=2,
∴点M在以N为圆心,2为半径的圆上.易知当点M在ON上时,OM最小,最小值为2,
∴线段OM 长的最小值为2.故选A.
A 设OP与⊙O交于点N,连接MN,OQ,如图.

∵OP=8,ON=4,
∴N是OP的中点.又
∵M是PQ的中点,
∴MN为△POQ的中位线,
∴MN=$\frac{1}{2}$OQ=$\frac{1}{2}$× 4=2,
∴点M在以N为圆心,2为半径的圆上.易知当点M在ON上时,OM最小,最小值为2,
∴线段OM 长的最小值为2.故选A.
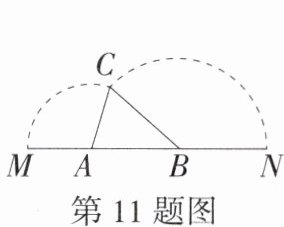
11.「★☆」如图,已知A,B是线段MN上的两点,MN= 4,MA= 1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M,N两点重合成一点C,构成△ABC,设AB= x.若以点B为圆心,1.6为半径作⊙B,使点M和点N都在⊙B外,则x的取值范围是(
A.1<x<2
B.0.6<x<1.6
C.1<x<1.6
D.1<x<1.4
D
)
A.1<x<2
B.0.6<x<1.6
C.1<x<1.6
D.1<x<1.4
答案:
D
∵MN=4,MA=1,AB=x,
∴BN=4−1−x=3−x.
∵以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M,N两点重合成一点C,构成△ABC,
∴AC=AM=1,BC=BN=3−x.
∴1+3−x>x,1+x>3−x,
∴1<x<2.
∵以点B为圆心,1.6为半径作⊙B,使点M 和点N都在⊙B外,
∴1+x>1.6且3−x>1.6,
∴0.6<x<1.4,
∴x的取值范围是1<x<1.4.故选D.
∵MN=4,MA=1,AB=x,
∴BN=4−1−x=3−x.
∵以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M,N两点重合成一点C,构成△ABC,
∴AC=AM=1,BC=BN=3−x.
∴1+3−x>x,1+x>3−x,
∴1<x<2.
∵以点B为圆心,1.6为半径作⊙B,使点M 和点N都在⊙B外,
∴1+x>1.6且3−x>1.6,
∴0.6<x<1.4,
∴x的取值范围是1<x<1.4.故选D.
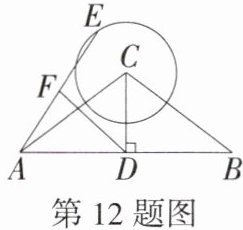
12.「2025江苏无锡江阴高新实验中学月考,★☆」如图,△ABC中,AC= BC,CD是△ABC的高,AB= 8,CD= 3,则BC= ______;若以点C为圆心,2为半径作⊙C,点E是⊙C上一动点,连接AE,点F是AE的中点,则线段DF长度的最小值是______.

答案:
5;$\frac{3}{2}$ 解析
∵AC=BC,CD是△ABC的高,
∴BD=$\frac{1}{2}$AB=4,CD⊥AB,
∴BC=$\sqrt{BD^2+CD^2}$=5. 如图,连接BE,CE,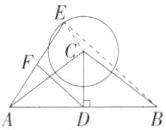
∵点F是AE的中点,点D是AB的中点,
∴DF是△AEB的中位线,
∴DF=$\frac{1}{2}$BE,易知当E、C、B三点共线,且E点在线段BC上时,线段BE的长最小,此时线段DF的长最小,
∵BE的最小值=BC−CE=5−2=3,
∴线段DF长度的最小值为$\frac{3}{2}$
5;$\frac{3}{2}$ 解析
∵AC=BC,CD是△ABC的高,
∴BD=$\frac{1}{2}$AB=4,CD⊥AB,
∴BC=$\sqrt{BD^2+CD^2}$=5. 如图,连接BE,CE,

∵点F是AE的中点,点D是AB的中点,
∴DF是△AEB的中位线,
∴DF=$\frac{1}{2}$BE,易知当E、C、B三点共线,且E点在线段BC上时,线段BE的长最小,此时线段DF的长最小,
∵BE的最小值=BC−CE=5−2=3,
∴线段DF长度的最小值为$\frac{3}{2}$
13.「2025江苏盐城阜宁实验中学月考,★☆」设⊙O的半径为2,点P到圆心的距离OP= m,且m使关于x的方程$2x^2-2√{2}x+m-1= 0$有两个不相等的实数根,试确定点P与⊙O的位置关系.
答案:
解析 由题意可知$(-2\sqrt{2})^2$−4×2×(m−1)>0,解得m<2,又
∵⊙O的半径为2,
∴点P在⊙O内
∵⊙O的半径为2,
∴点P在⊙O内
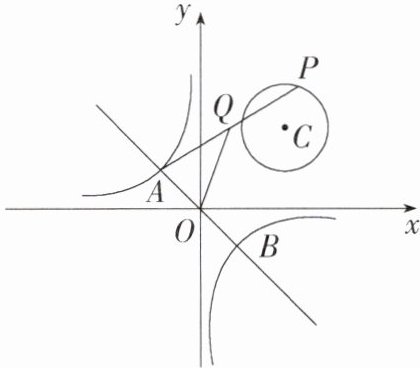
14.新几何直观「2025江苏盐城阜宁实验中学月考,★☆」如图,在平面直角坐标系中,直线y= -x与双曲线y= kx(k≠0)交于A、B两点,P是以点C(2,2)为圆心,1为半径的圆上的动点,连接AP,Q为AP的中点.若线段OQ长度的最大值为2,求k的值.

答案:
解析 连接BP(图略),由题意可知,OQ是△ABP的中位线,所以OQ=$\frac{1}{2}$BP,当B、C、P三点共线,且点C 在线段BP上时,PB的长有最大值,因为OQ的最大值为2,所以BP的最大值为4,此时BC=BP−PC=4−1=3,设点B(m,−m),则$(2−m)^2$+[2−(−m)]^2=3^2,所以m^2=$\frac{1}{2}$,因为点B(m,−m)在双曲线y=$\frac{k}{x}$(k≠0)上,所以k=−m^2=−$\frac{1}{2}$.
查看更多完整答案,请扫码查看


