《2025年5年中考3年模拟九年级数学全一册苏科版》

1.「2024甘肃甘南中考」如图,AB是⊙O的直径,DB,DE分别切⊙O于点B,C,若∠ACE= 18°,则∠D的度数是( )


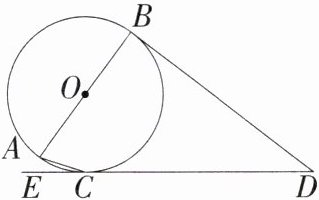
A.18°
B.36°
C.48°
D.72°

答案：
B　连接BC,如图，
∵ DB、DE分别切⊙O于点B、C,
∴ BD=DC,
∴ ∠DBC=∠DCB,
∵ AB是⊙O的直径,
∴ ∠ACB=90°,
∵ ∠ACE=18°,
∴ ∠DCB=90° - 18°=72°,
∴ ∠D=180° - 72°×2=36°.故选B.

2.「2023广东广州中考」如图,△ABC的内切圆⊙I与BC,CA,AB分别相切于点D,E,F,若⊙I的半径为r,∠A= α,则BF+CE-BC的值和∠FDE的大小分别为( )


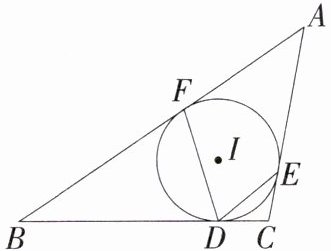
A.2r,90°-α
B.0,90°-α
C.2r,90°- $\frac{α}{2}$
D.0,90°- $\frac{α}{2}$

答案：
D　如图,连接IF,IE.
∵ △ABC的内切圆⊙I与BC,CA,AB分别相切于点D,E,F,
∴ BF=BD,CD=CE,IF⊥AB,IE⊥AC,
∴ BF+CE - BC=BD+CD - BC=BC - BC=0,∠AFI=∠AEI=90°,
∴ ∠EIF=180° - α,
∴ ∠EDF=$\frac{1}{2}$∠EIF=90° - $\frac{\alpha}{2}$.故选D.

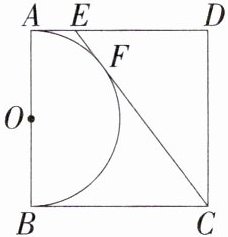
3.「2025江苏南京外国语学校月考」如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AD边于点E,若△CDE的周长为12,则直角梯形ABCE的周长为14.

答案： 14
解析　设AE的长为x,
∵ CE与半圆O相切于点F,
∴ AE=EF,BC=FC,
∵ EF+FC+CD+ED=12,
∴ AE+ED+CD+BC=12,
∴ AD+CD+BC=12,
∵ AD=CD=BC=AB,
∴ 正方形ABCD的边长为4，
在Rt△CDE中,ED²+CD²=CE²,
即(4 - x)²+4²=(4 + x)²,解得x=1,
∴ AE+EF+FC+BC+AB=14,
∴ 直角梯形ABCE的周长为14.

4.「2025江苏南京鼓楼期中」如图,四边形ABCD是⊙O的外切四边形,且BC= 3,AD= 5,若四边形ABCD的面积等于15,则⊙O的半径为______.

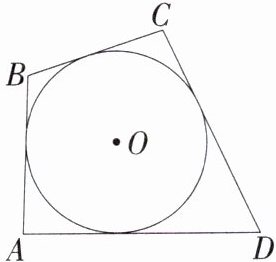
答案：
$\frac{15}{8}$
解析　如图，连接OA、OB、OC、OD,设四边形ABCD与⊙O的切点分别为E、F、G、H,连接OE、OF、OG、OH,则OE⊥AB,OF⊥AD,OG⊥CD,OH⊥BC,由切线长定理得AE=AF,DF=DG,CG=CH,BE=BH,
∴ AB+CD=BC+AD=16,设⊙O的半径为r,由题意得$\frac{1}{2}$AB·r+$\frac{1}{2}$BC·r+$\frac{1}{2}$AD·r+$\frac{1}{2}$CD·r=15,即$\frac{1}{2}$(AB+BC+AD+CD)·r=15,
∴ r=$\frac{15}{8}$,

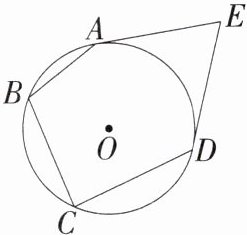
5.「2024四川泸州中考,★☆」如图,EA,ED是⊙O的切线,切点为A,D,点B,C在⊙O上,若∠BAE+∠BCD= 236°,则∠E= ( )


A.56°
B.60°
C.68°
D.70°

答案：
C　连接AD,如图,
∵ 四边形ABCD是⊙O的内接四边形,
∴ ∠BAD+∠BCD=180°,
∵ ∠BAE+∠BCD=236°,
∴ ∠EAD+∠BAD+∠BCD=∠EAD+180°=236°,
∴ ∠EAD=56°,
∵ EA,ED是⊙O的切线,
∴ EA=ED,
∴ ∠EDA=∠EAD=56°,
∴ ∠E=180° - ∠EDA - ∠EAD=180° - 56° - 56°=68°,故选C.

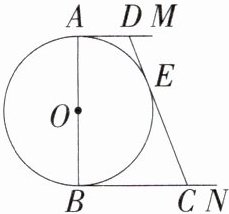
6.「2025江苏扬州宝应期末,★☆」如图,⊙O的直径AB的长度为定值a,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别交于点D,C,设AD= x,BC= y,当x,y的值变化时,下列代数式的值不变的是( )


A.x-y
B.x+y

C.xy
$D.x^2+y^2$

答案：
C　如图,过D作DF⊥BN于F.
∵ AM、BN与⊙O分别相切于点A、B,
∴ AB⊥AM,AB⊥BN,又
∵ DF⊥BN,
∴ ∠BAD=∠ABC=∠BFD=90°,
∴ 四边形ABFD是矩形,
∴ BF=AD=x,DF=AB=a,
∵ BC=y,
∴ FC=BC - BF=y - x.
∵ DE切⊙O于E,
∴ DE=DA=x,CE=CB=y,
∴ DC=DE+CE=x+y,
在Rt△DFC中,由勾股定理得(x + y)²=(y - x)²+a²,
∴ xy=$\frac{a²}{4}$,
∴ 代数式的值不变的是xy,故选C.

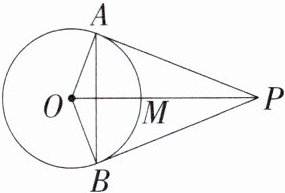
7.「2025江苏南京联合体期中,★☆」如图,已知PA,PB是⊙O的两条切线,A,B为切点,线段OP交⊙O于点M.给出下列四种说法：①PA= PB；②OP⊥AB；③四边形OAPB有外接圆；④M是△ABP的内心.其中,正确的个数是( )


A.1
B.2
C.3
D.4

答案：
D
∵ PA,PB是⊙O的两条切线,
∴ PA=PB,∠OAP=∠OBP=90°,故①正确;
∵ OA=OB,PA=PB,
∴ OP⊥AB,故②正确;
连接AM,BM,如图所示.
∵ ∠OAB+∠PAB=∠APM+∠PAB=90°,
∴ ∠OAB=∠APM,
∵ OA=OM,
∴ ∠OAM=∠OMA,
∴ ∠OAB+∠BAM=∠APM+∠PAM,
∴ ∠BAM=∠PAM,即AM平分∠BAP,
同理可得BM平分∠ABP,
∴ M是△ABP的内心,故④正确;取OP的中点Q,连接AQ,BQ,
则AQ=$\frac{1}{2}$OP=BQ,即QA=QO=QP=QB,
∴ B,O,A,P四点共圆,故③正确.故选D.