《2025年5年中考3年模拟九年级数学全一册苏科版》

9. 多解法「2024 四川达州中考,」抛物线$y= -x^{2}+bx+c$与x轴交于两点,其中一个交点的横坐标大于1,另一个交点的横坐标小于1,则下列结论正确的是(A)
A.$b+c＞1$
B.$b= 2$
C.$b^{2}+4c＜0$
D.$c＜0$

答案： A设抛物线y=−x²+bx+c与x轴交于两点,分别为(x₁,0)和(x₂,0),且x₁＜1,x₂＞1. [解法一]根与系数关系法:
∵x₁＜1,x₂＞1,
∴x₁−1＜0,x₂−1＞0,
∴(x₁−1)(x₂−1)＜0,
∴x₁x₂−(x₁+x₂)+1＜0,由根与系数的关系可得,−c−b+1＜0,
∴b+c＞1.故选A. [解法二]图像法:
∵y=−x²+bx+c的图像开口向下,
∴当x=1时,y=−1+b+c＞0,
∴b+c＞1.故选A.

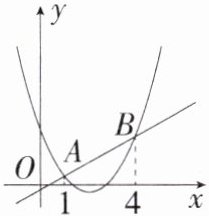
10.「2025 江苏昆山水平测试,」如图,直线$y= kx+t(k≠0)与抛物线y= ax^{2}+bx+c(a≠0)交于A(1,m),B(4,n)$,则不等式$ax^{2}+(b-k)x+c-t＜0$的解集是1＜x＜4。

答案： 答案　1＜x＜4 解析　由ax²+(b−k)x+c−t＜0得ax²+bx+c＜kx+t.
∵直线y=kx+t(k≠0)与抛物线y=ax²+bx+c(a≠0) 交于A(1,m),B(4,n),
∴不等式ax²+bx+c＜kx+t的解集是1＜x＜4,
∴不等式ax²+(b−k)x+c−t＜0的解集是1＜x＜4, 故答案为1＜x＜4.

11.「」已知关于x的二次函数$y= kx^{2}+(2k-1)x-2$(k为常数)的图像与x轴的两个交点横坐标异号,且距离等于3,则k的值为1。

答案： 答案　1 解析　设kx²+(2k−1)x−2=0的两根为x₁,x₂,则x₁+x₂=−$\frac{2k - 1}{k}$,x₁x₂=−$\frac{2}{k}$.
∴(x₁−x₂)²=(x₁+x₂)²−4x₁x₂=$\frac{(2k + 1)²}{k²}$.
∵函数y的图像与x轴的两个交点间的距离等于3,
∴|x₁−x₂|=3,
∴$\frac{(2k + 1)²}{k²}$=3², 解得k=1或k=−$\frac{1}{5}$.
∵函数y的图像与x轴的两个交点横坐标异号,
∴x₁x₂=−$\frac{2}{k}$＜0,
∴k=1.

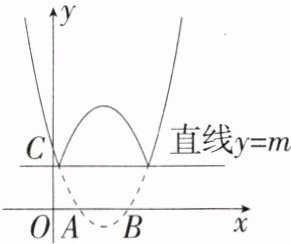
12.「」如图,已知抛物线$y= ax^{2}+bx+c$(a,b,c为常数,$a≠0$)交x轴于$A(1,0)$、$B(3,0)$两点,交y轴于$C(0,3)$,将该抛物线位于直线$y= m$(m为常数,$m≥0$)下方的部分沿直线$y= m$翻折,其余部分不变,得到的新图像记为“图像W”。
(1)求该抛物线的表达式。
(2)当$m= 0$时,直线$y= x+n$与图像W有三个交点,求n的值。

答案：
(1)由题意得$\begin{cases}a + b + c = 0\\9a + 3b + c = 0\\c = 3\end{cases}$ 解得$\begin{cases}a = 1\\b = - 4\\c = 3\end{cases}$
∴该抛物线的表达式为y=x²−4x+3.
(2)m=0时,由图像得,当直线y=x+n与图像W有三个交点时，存在两种情况: ①当直线y=x+n过点A时,与图像W有三个交点，此时n=−1; ②当直线y=x+n与图像W位于线段AB上方部分对应的函数图像相切时，与图像W有三个交点，此时x+n=−x²+4x−3,x²−3x+n+3=0,b²−4ac=(−3)²−4×1×(n+3)=0,
∴n=−$\frac{3}{4}$. 综上,n的值是−1或−$\frac{3}{4}$.

13. 运算能力「2025 北京海淀期中」如图,在平面直角坐标系xOy中,抛物线$y= 3x^{2}+bx+c$与x轴交于A,B两点,且$AB= 4$。若将此抛物线先向左平移2个单位,再向下平移m个单位,所得新抛物线与x轴两个交点间的距离为8,则m的值为(D)
A.6
B.2
C.24
D.36

答案： D　当y=0时,设y=3x²+bx+c=0的两根分别为x₁、x₂,则x₁+x₂=−$\frac{b}{3}$,x₁x₂=$\frac{c}{3}$.
∵AB=4,
∴|x₁−x₂|=4,
∴(x₁−x₂)²=(x₁+x₂)²−4x₁x₂=16,
∴b²−12c=144.
∵所得新抛物线与x轴两个交点间的距离为8,即当y=m时,抛物线上两点之间距离为8,设3x²+bx+c=m的两根分别为x₃、x₄,则x₃+x₄=−$\frac{b}{3}$,x₃x₄=$\frac{c - m}{3}$,
∴|x₃−x₄|=8,
∴(x₃−x₄)²=(x₃+x₄)²−4x₃x₄=64,
∴b²−12×(c−m)=b²−12c+12m=576,
∵b²−12c=144,
∴144+12m=576,解得m=36.故选D.

14. 推理能力 代数推理「2024 江苏南京联合体一模」已知二次函数$y= ax^{2}+bx+2(a＜0)$。
(1)求证：该函数的图像与x轴总有两个公共点。
(2)若该函数图像与x轴的两个交点坐标分别为$(x_{1},0)$、$(x_{2},0)$,且$x_{2}= -2x_{1}$,求证：$a+b^{2}= 0$。
(3)若$A(k,y_{1}),B(6,y_{2}),C(k+4,y_{1})$都在该二次函数的图像上,且$2＜y_{2}＜y_{1}$,结合函数的图像,直接写出k的取值范围。

答案：
(1)证明:由题意得b²−4a×2=b²−8a.
∵a＜0,
∴−8a＞0.又对于任意的实数b都有b²≥0,
∴b²−8a＞0,
∴该函数的图像与x轴总有两个公共点.
(2)证明:由题意得,x₁+x₂=−$\frac{b}{a}$,x₁x₂=$\frac{2}{a}$.
∵x₂=−2x₁,
∴x₁=$\frac{b}{a}$,x₂=−$\frac{2b}{a}$.
∵x₁x₂=$\frac{2}{a}$,
∴−$\frac{2b²}{a²}$=$\frac{2}{a}$,
∴−b²=a.
∴a+b²=0.
(3)由题意知,该函数图像的对称轴是直线x=$\frac{k + k + 4}{2}$=k+2. 令x=0,则y=2.
∵a＜0,
∴当抛物线上的点离对称轴越近函数值越大. 又2＜y₂＜y₁,
∴|k+2−0|＞|k+2−6|＞|k+2−k|.
∴|k+2|＞|k−4|＞2. ①当k＜−2时,−k−2＞4−k＞2,
∴无解. ②当−2≤k≤4时,k+2＞4−k＞2,
∴1＜k＜2. ③当k＞4时,k+2＞k−4＞2,
∴k＞6. 综上,1＜k＜2或k＞6.