《2025年5年中考3年模拟九年级数学全一册苏科版》

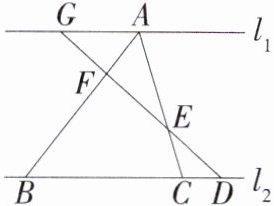
7.「2024江苏无锡锡山钱桥中学月考」如图$,l_1//l_2,AF$：BF= 2：5,BC：CD= 4：1,则AE：EC的值为(C)

A.$\frac {5}{2}$
B.$\frac {1}{4}$
C.2
D.$\frac {3}{2}$

答案： C

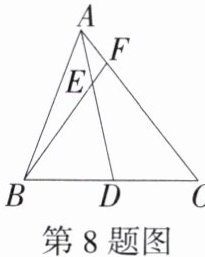
8.「2025江苏南通崇川田家炳中学月考」如图,AD是△ABC的中线,E是AD上一点,AE= $\frac {1}{4}$AD,BE的延长线交AC于F,则$\frac {AF}{AC}$的值为______$\frac{1}{7}$.

答案： $\frac{1}{7}$

9.「2025四川成都英才学校月考」如图,点D、E分别在△ABC的边AB,AC上,且DE//BC,过点A作AG//BC,分别交∠AED,∠ACB的平分线于点F,G.若BD= 2AD,CG平分线段BD,则FG：BC= $\frac{4}{3}$.

答案： $\frac{4}{3}$

10.「2024广东深圳中学期中」如图,在Rt△ABC中,∠ACB= 90°,AB= 4,点D,E分别在边AB,AC上,且DB= 2AD,AE= 3EC,连接BE,CD,BE与CD相交于点O,则△ABO面积的最大值为$\frac{8}{3}$.

答案： $\frac{8}{3}$

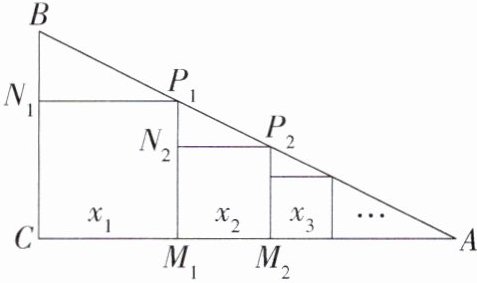
11.新推理能力新规律探究题「2024江苏无锡宜兴丁蜀月考」如图,在Rt△ABC中,∠C= 90°,BC= 1,AC= 2,把边长分别为$x_1,x_2,x_3,…,xₙ$的n个正方形依次放入△ABC中,第1个正方形$CM_1P_1N_1$的顶点分别放在Rt△ABC的各边上；第2个正方形$M_1M_2P_2N_2$的顶点分别放在$Rt△AP_1M_1$的各边上；……,其他正方形依次放入,则第2023个正方形的边长$x_2₀_2_3$为______$(\frac{2}{3})^{2023}$.

答案： $(\frac{2}{3})^{2023}$

12.新推理能力【认识模型】
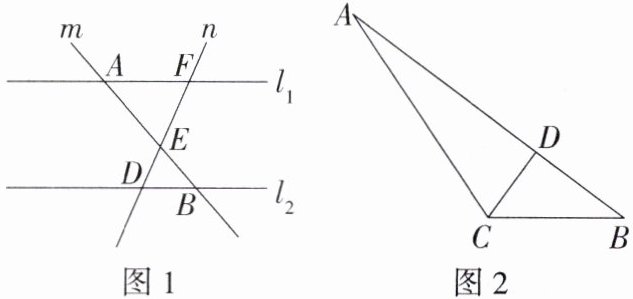
(1)如图1,直线l₁//l₂,直线m、n分别与l₁,l₂交于点A,B和点F,D,m和n交于点E,则$\frac {BE}{AB}$=$\frac{DE}{FD}$.
【应用模型】
(2)如图2,在△ABC中,D是边AB上一点,且$\frac {BD}{AB}= \frac {CD}{AC}= \frac {1}{3}$,若BC= 4,AB= 10,求AC的长.$2\sqrt{13}$

答案：
(1)$\frac{DE}{FD}$；
(2)$2\sqrt{13}$