《2025年5年中考3年模拟九年级数学全一册苏科版》

1. 「2024 广东中考」长江是中华民族的母亲河,长江流域孕育出藏羌文化、巴蜀文化、荆楚文化、吴越文化等区域文化。若从上述四种区域文化中随机选一种文化开展专题学习,则选中“巴蜀文化”的概率是(A)
A.$\frac{1}{4}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{3}{4}$

答案： A 根据题意，得选中“巴蜀文化”的概率是$\frac{1}{4}$，故选A.

2. 新课标 中华优秀传统文化「2024 广东深圳中考」二十四节气,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律,二十四个节气分别为春季(立春、雨水、惊蛰、春分、清明、谷雨),夏季(立夏、小满、芒种、夏至、小暑、大暑),秋季(立秋、处暑、白露、秋分、寒露、霜降),冬季(立冬、小雪、大雪、冬至、小寒、大寒),若从二十四个节气中选一个节气,则抽到的节气在夏季的概率为(D)
A.$\frac{1}{24}$
B.$\frac{1}{12}$
C.$\frac{1}{6}$
D.$\frac{1}{4}$

答案： D 从二十四个节气中选一个节气，则抽到的节气在夏季的概率为$\frac{6}{24}=\frac{1}{4}$，故选D.

3. 学科特色 方程思想「2025 江苏扬州邗江梅苑双语学校期中」一个不透明布袋里装有 4 个红球和 5 个白球,现在放进去 n 个黄球(仅有颜色不同)。若从中任意摸出 1 个球是黄球的概率为$\frac{1}{4}$,则 n = 3。

答案： 答案 3 解析 由题意得$\frac{n}{4+5+n}=\frac{1}{4}$，解得$n=3$，经检验，$n=3$是原方程的解，且符合题意.

4. 「2024 青海西宁中考」在一个不透明的袋中装有 5 个相同的小球,分别写有$\sqrt{0.2}$,$\sqrt{\frac{1}{3}}$,$\sqrt{6}$,$\sqrt{10}$,$\sqrt{27}$,随机摸出一个小球,上面的二次根式是最简二次根式的概率是$\frac{2}{5}$。

答案： 答案 $\frac{2}{5}$ 解析 $\sqrt{0.2},\sqrt{\frac{1}{3}},\sqrt{6},\sqrt{10},\sqrt{27}$这5个二次根式中，$\sqrt{6},\sqrt{10}$是最简二次根式，共2个，$\therefore$随机摸出1个小球，上面的二次根式是最简二次根式的概率是$\frac{2}{5}$.

5. 跨学科 物理 电路图「2024 江苏盐城亭湖景山中学月考,★☆」如图所示,电路图上有 A、B、C 三个开关和一个小灯泡,闭合开关 C 或者同时闭合开关 A、B,都可以使小灯泡发光,现在任意闭合其中一个开关,则小灯泡发光的概率等于$\frac{1}{3}$。

答案： 答案 $\frac{1}{3}$ 解析 $\because$闭合开关C或者同时闭合开关A、B，都可以使小灯泡发光，$\therefore$任意闭合其中一个开关共有3种等可能的结果，而能使小灯泡发光的只有闭合开关C，$\therefore$所求概率等于$\frac{1}{3}$.

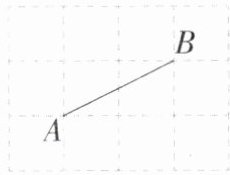
6. 「2025 江苏南师附中宿迁分校月考,★☆」如图,点 A,B 在由边长为 1 的小正方形组成的网格的格点上,在网格格点中除点 A,B 外任取一点 C,则使△ABC 的面积为 1 的概率是$\frac{2}{9}$。

答案： 答案 $\frac{2}{9}$ 解析 如图， 任意放置一点C(除点A,B外)共有$20 - 2 = 18$种等可能的结果，其中能使$\triangle ABC$的面积为1的结果有4种，点$C_{1},C_{2},C_{3},C_{4}$均满足题意，$\therefore$使$\triangle ABC$的面积为1的概率为$\frac{4}{18}=\frac{2}{9}$.

7. 「2022 江苏镇江中考,★☆」从 2 021、2 022、2 023、2 024、2 025 这五个数中任意抽取 3 个数,抽到中位数是 2 022 的 3 个数的概率等于$\frac{3}{10}$。

答案： 答案 $\frac{3}{10}$ 解析 从2021、2022、2023、2024、2025这五个数中任意抽取3个数为2021、2022、2023；2021、2022、2024；2021、2022、2025；2021、2023、2024；2021、2023、2025；2021、2024、2025；2022、2023、2024；2022、2023、2025；2022、2024、2025；2023、2024、2025.共有10种等可能的情况，其中中位数是2022的有3种，$\therefore$抽到中位数是2022的3个数的概率为$\frac{3}{10}$，故答案为$\frac{3}{10}$.

8. 新课标 几何直观 小明用大小和形状都完全一样的正方体按照一定规律摆放了一组图案(如图所示),每个图案中他只在最下面的正方体上写“心”字,寓意“不忘初心”。其中第(1)个图案中有 1 个正方体,第(2)个图案中有 3 个正方体,第(3)个图案中有 6 个正方体,……,按照此规律,从第(100)个图案所需正方体中随机抽取一个正方体,抽到带“心”字正方体的概率是______$\frac{2}{101}$。

答案： 答案 $\frac{2}{101}$ 解析 $\because$第
(1)个图案中正方体的个数为1，第
(2)个图案中正方体的个数为$3 = 1 + 2$，第
(3)个图案中正方体的个数为$6 = 1 + 2 + 3$，$\therefore$第
(100)个图案中，正方体一共有$1 + 2 + 3 + \cdots + 99 + 100 = \frac{(1 + 100)×100}{2} = 5050$(个)，其中写有“心”字的正方体有100个，$\therefore$所求概率是$\frac{100}{5050}=\frac{2}{101}$.