《2025年5年中考3年模拟九年级数学全一册苏科版》

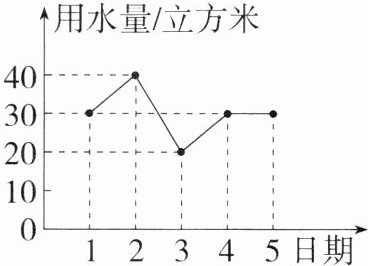
1. 「2023浙江湖州中考」某住宅小区6月1日~6月5日每天用水量情况如图所示,那么这5天平均每天的用水量是(B)

A.25立方米
B.30立方米
C.32立方米
D.35立方米

答案： B 由折线统计图可知,该小区这五天的用水量的数据分别是30、40、20、30、30,所以这5天平均每天的用水量为$\frac{1}{5} × (30+40+20+30+30)=30$(立方米).故选B.

2. 「2024江苏宿迁中考」一组数据6,8,10,x的平均数是9,则x的值为______。12

答案： 答案 12 解析
∵一组数据6,8,10,x的平均数是9,
∴$\frac{6+8+10+x}{4}=9$,解得$x=12$.

3. 如果一组数据$x_{1},x_{2},x_{3},…,x_{n}$的平均数是5,则数据$2x_{1}+3,2x_{2}+3,2x_{3}+3,…,2x_{n}+3$的平均数为______13。

答案： 答案 13 解析
∵$x_{1},x_{2},x_{3},\cdots,x_{n}$的平均数是5,
∴$x_{1}+x_{2}+x_{3}+\cdots+x_{n}=5n$,
∴$2x_{1}+3+2x_{2}+3+2x_{3}+3+\cdots+2x_{n}+3=2×5n+3n=13n$,
∴$2x_{1}+3,2x_{2}+3,2x_{3}+3,\cdots,2x_{n}+3$的平均数=$\frac{13n}{n}=13$.

4. 「2025江苏盐城东台期中」某快递公司快递员六月第三周投放快递物品的数量如下：有3天是20件,有1天是31件,有3天是35件,则本周的日平均投递物品数量为(D)
A.31件
B.30件
C.29件
D.28件

答案： D 由题意可得,本周的日平均投递物品数量为$\frac{20×3+31×1+35×3}{3+1+3}=28$(件).故选D.

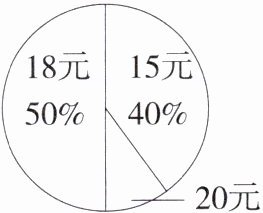
5. 「2024江苏南京建邺期中」学校食堂有15元,18元,20元三种盒饭供学生选择(每人购一份)。某天盒饭销售情况如图所示,则当天学生购买盒饭费用的平均数是(C)

A.15元
B.16元
C.17元
D.18元

答案： C $15×40\%+18×50\%+20×(1-40\%-50\%)=17$(元),即当天学生购买盒饭费用的平均数是17元.故选C.

6. 「2025江苏南京期末」学校开展了纪念“一二·九”运动的合唱比赛,其中评分项目为歌曲内容、精神面貌和艺术效果,并依次按照2:3:5计算综合成绩。某班这三项分别得了90分、90分和88分,则该班的综合成绩是89分。

答案： 答案 89 解析 由题意得该班的综合成绩为$\frac{90×2+90×3+88×5}{2+3+5}=89$(分).

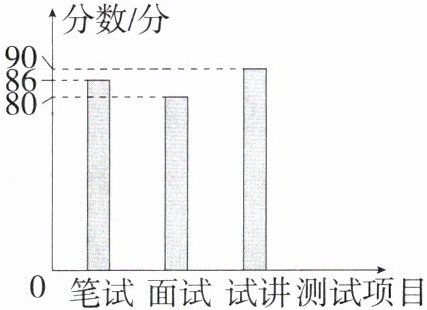
7. 「2024四川德阳中考」某校拟招聘一名优秀的数学教师,设置了笔试、面试、试讲三项水平测试,综合成绩按照笔试占30%,面试占30%,试讲占40%进行计算,小徐的三项测试成绩如图所示,则她的综合成绩为85.8分。

答案： 答案 85.8 解析 她的综合成绩为$86×30\%+80×30\%+90×40\%=85.8$(分).

8. 「2025云南昭通永善期中,☆」已知甲糖果的单价为m元,乙糖果的单价为10元,则2千克甲糖果和n千克乙糖果混合而成的什锦糖果的单价为(C)
A.$\frac{m+10}{2}$元
B.$\frac{2+n}{2}$元
C.$\frac{2m+10n}{2+n}$元
D.$\frac{2m+10n}{m+10}$元

答案： C 依题意得,混合而成的什锦糖果的总价为$(2m+10n)$元,总质量为$(2+n)$千克,故混合而成的什锦糖果的单价为$\frac{2m+10n}{2+n}$元.故选C.

9. 「2024江苏苏州高新区一模,☆」某次射击训练中,一小组的成绩如表所示：
|环数|6|7|8|9|
|人数|1|3| |2|
若该小组的平均成绩为7.7环,则成绩为8环的人数是(B)
A.3
B.4
C.5
D.6

答案： B 设成绩为8环的人数是x,根据题意得$(6×1+7×3+8x+9×2)÷(1+3+x+2)=7.7$,解得$x=4$,经检验,$x=4$是原方程的解,则成绩为8环的人数是4.故选B.