《2025年实验班提优训练九年级数学上册人教版》

1. (2024·成都中考)在平面直角坐标系 $ xOy $ 中,点 $ P(1,-4) $ 关于原点对称的点的坐标是(B).
A. $ (-1,-4) $
B. $ (-1,4) $
C. $ (1,4) $
D. $ (1,-4) $

答案： B

2. 实验班原创 在平面直角坐标系中,点 $ P(-6,1) $ 与点 $ Q(6,-1) $ 的位置关系是(C).
A. 关于 $ x $ 轴对称
B. 关于 $ y $ 轴对称
C. 关于原点对称
D. 没有对称关系

答案： C

3. 教材 P70 习题 T4·变式 在平面直角坐标系中,点 $ (a+2,2) $ 关于原点的对称点为 $ (4,-b) $,则 $ ab $ 的值为(D).
A. $ -4 $
B. $ 4 $
C. $ 12 $
D. $ -12 $

答案： D

4. 在平面直角坐标系中,若点 $ P(2,-1) $ 与点 $ Q(-2,m) $ 关于原点对称,则 $ m $ 的值是______1.

答案： 1

5. (2025·广东广州期中)若点 $ (a,-9) $ 与 $ (3,b) $ 关于原点对称,则 $ a+b= $______6.

答案： 6

6. (2025·安徽芜湖无为期中)已知点 $ M(3m-2,2m+1) $,解答下列问题：
(1)若点 $ M $ 与点 $ (-7,-7) $ 关于原点对称,求 $ m $ 的值；
(2)若点 $ N(3,9) $,且直线 $ MN $ 平行于 $ x $ 轴,求点 $ M $ 的坐标.

答案：
(1)
∵点M(3m−2,2m+1)与点(−7,−7)关于原点对称，
∴$\begin{cases}3m - 2 = 7\\2m + 1 = 7\end{cases}$，解得m=3。
(2)
∵点N(3,9)，且直线MN平行于x轴，
∴点M的纵坐标为9，
∴2m+1=9，解得m=4，
∴点M的坐标为(10,9)。

7. (2024·陕西中考)一个正比例函数的图象经过点 $ A(2,m) $ 和点 $ B(n,-6) $. 若点 $ A $ 与点 $ B $ 关于原点对称,则这个正比例函数的表达式为(A).
A. $ y= 3x $
B. $ y= -3x $
C. $ y= \frac{1}{3}x $
D. $ y= -\frac{1}{3}x $

答案： A　[解析]
∵点A(2,m)和点B(n,−6)关于原点对称，
∴m=6，
∴点A的坐标为(2,6)。设正比例函数的表达式为y=kx(k≠0)，
∵点A(2,6)在正比例函数y=kx的图象上，
∴6=2k，解得k=3，
∴这个正比例函数的表达式为y=3x。故选A。

8. 数形结合思想(浙江宁波余姚中学自主招生)在平面直角坐标系中,已知点 $ P(a,b)(|a| \neq |b|) $,设点 $ P $ 关于直线 $ y= x $ 的对称点为 $ Q $,点 $ P $ 关于原点的对称点为 $ R $,则 $ \triangle PQR $ 的形状是( ).
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 不能确定

答案：
B　[解析]如图，根据平面直角坐标系内关于y=x对称的点的特点，得OQ=OP，
∴∠OPQ=∠OQP。
∵点P，R关于原点对称，
　　　　　　　　　　　　　
∴OP=OR，
∴OQ=OR，
∴∠ORQ=∠OQR。
∵∠OPQ+∠OQP+∠ORQ+∠OQR=180°，
∴2(∠OQP+∠OQR)=180°，
∴∠PQR=90°，
∴△PQR为直角三角形。故选B。

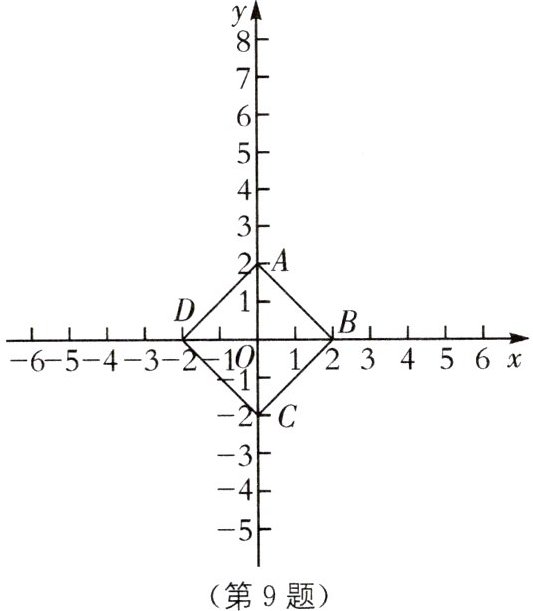
9. (2025·四川成都期中)在平面直角坐标系 $ xOy $ 中,点 $ A(0,2) $,点 $ B(2,0) $,点 $ C(0,-2) $,点 $ D(-2,0) $,$ M $ 为四边形 $ ABCD $ 边上一点. 对于点 $ P(6,0) $,给出如下定义：若 $ \angle PMP_1= 90^{\circ} $,$ PM= P_1M $,点 $ P_1 $ 在 $ x $ 轴下方,点 $ P_1 $ 关于原点的对称点为 $ Q $,我们称点 $ Q $ 为点 $ P $ 关于点 $ M $ 为直角顶点的“变换点”；则 $ P $ 关于点 $ B $ 为直角顶点的“变换点”坐标为______；若直线 $ y= kx+3k(k \neq 0) $ 上存在点 $ P $ 关于点 $ M $ 为直角顶点的“变换点”,则 $ k $ 的取值范围为______.

答案：
(−2,4)　$\frac{4}{5}\leqslant k\leqslant8$　[解析]如图，P(6,0)，B(2,0)，∠PBT=90°，
∴PB=6−2=4。
∵∠PBT=90°，PB=TB，
∴T(2,−4)，
∴R，T关于原点对称，
∴R(−2,4)，
∴P关于点B为直角顶点的“变换点”坐标为R(−2,4)。如图，∠PAK=90°，AK=PA，过点K作KE⊥y轴于点E，
∴∠AEK=∠POA=90°，
∴∠APO+∠OAP=90°。
∵∠PAK=90°，
∴∠KAE+∠OAP=90°，
∴∠KAE=∠APO，在△AEK和△POA中，$\begin{cases}\angle KAE = \angle APO\\\angle AEK = \angle POA\\AK = PA\end{cases}$，
∴△AEK≌△POA(AAS)。
∴KE=OA=2，AE=PO=6，
∴OE=6−2=4，
∴K(−2,−4)。
∵点K关于原点的对称点为G，
∴G(2,4)，即P关于点A为直角顶点的“变换点”坐标为G(2,4)，同理，点P关于点D为直角顶点的“变换点”坐标为F(2,8)，点P关于点C为直角顶点的“变换点”坐标为H(−2,8)。
　　　　
故点P关于点M为直角顶点的“变换点”的轨迹为正方形RGFH，
∵直线y=kx+3k上存在点P关于点M为直角顶点的“变换点”，
∴直线y=kx+3k与正方形RGFH的边有交点。
∵当y=0时，kx+3k=0，解得x=−3，
∴直线y=kx+3k(k≠0)经过定点(−3,0)。
　(ⅰ)当直线经过H(−2,8)时，
∴−2k+3k=8，解得k=8。
　(ⅱ)当直线经过G(2,4)时，
∴2k+3k=4，解得k=$\frac{4}{5}$。
　综上所述，$\frac{4}{5}\leqslant k\leqslant8$。