《2025年实验班提优训练九年级数学上册人教版》

1. 传统文化 剪纸 (2024·哈尔滨中考)剪纸是我国最古老的民间艺术之一.下列剪纸图案中既是轴对称图形又是中心对称图形的是(D).

答案： D

2. 教材P67练习T1·变式 给出以下4个图形:①等边三角形;②平行四边形;③菱形;④正方形.其中既是轴对称图形又是中心对称图形的是③④.

答案： ③④

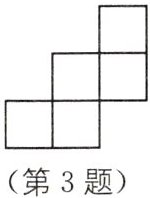
3. (2025·广东深圳光明区公明中学期中)如图,是由五个形状、大小都相同的正方形组成的图形,如果去掉其中一个正方形,使得剩下的图形是一个中心对称图形,那么不同的去法有____种.

答案：
2 [解析]去掉一个正方形,得到中心对称图形,如图所示,共2种方法

4. 中考新考法 满足条件的结论开放 (2025·贵州遵义期中)如图所示,网格中每个小正方形的边长为1,请你认真观察图(1)中的三个网格中阴影部分构成的图案,解答下列问题:

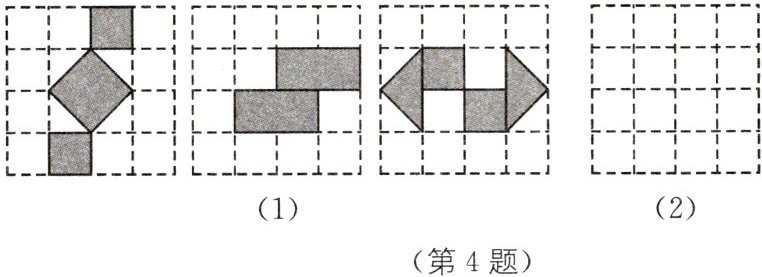
(1)这三个图案都具有以下共同特征:都是____对称图形,都不是____对称图形.
(2)请在图(2)中设计出一个面积为4,且具备上述特征的图案,要求所画图案不能与图(1)中所给出的图案相同.

答案：

(1)中心　轴
(2)设计出的图形，如图中的阴影部分所示(答案不唯一).
∵每个小正方形的边长为1,
∴图中阴影部分的面积为$4×\frac {1}{2}×1×1+2×1=4$.

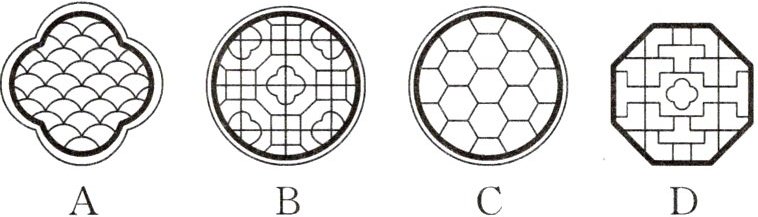
5. 传统文化 建筑砖雕 (2024·淮安中考)中国古典建筑中的镂空砖雕图案精美,下列砖雕图案中不是中心对称图形的是(A).

答案： A

6. 如图,在四边形ABCD中,$AB// CD$,$AB= CD$,对角线AC与BD交于点O,点E是AD的中点,连接OE,$\triangle ABD$的周长为12 cm,则下列结论错误的是(C).

A. $OE// AB$
B. 四边形ABCD是中心对称图形
C. $\triangle EOD$的周长等于3 cm
D. 若$∠ABC= 90^{\circ}$,则四边形ABCD是轴对称图形

答案： C [解析]
∵$AB// CD,AB=CD$,
∴四边形 ABCD 是平行四边形.
∵对角线 AC 与 BD 交于点 O,点 E 是 AD 的中点,
∴OE 是$△ABD$的中位线,
∴$OE// AB$,故 A 正确;
∵四边形 ABCD 是平行四边形,
∴四边形 ABCD 是中心对称图形,故 B 正确;
∵$△ABD$的周长为 12 cm,$\therefore C_{△EOD}=OE+OD+ED=\frac {1}{2}C_{△ABD}$,
∴$△EOD$的周长为 6 cm,故 C 错误;
若$∠ABC=90^{\circ }$,则四边形 ABCD 是矩形,是轴对称图形,故 D 正确.故选 C.

7. 如图,在菱形ABCD中,$AB= 6$,$∠A= 60^{\circ}$,将菱形ABCD沿菱形ABCD某一边所在直线平移a个单位长度,得到菱形$A_{1}B_{1}C_{1}D_{1}$;将菱形$A_{1}B_{1}C_{1}D_{1}沿菱形A_{1}B_{1}C_{1}D_{1}$某一边所在直线平移a个单位长度,得到菱形$A_{2}B_{2}C_{2}D_{2}$;将菱形$A_{2}B_{2}C_{2}D_{2}沿菱形A_{2}B_{2}C_{2}D_{2}$某一边所在直线平移a个单位长度,得到菱形$A_{3}B_{3}C_{3}D_{3}$.若四个菱形构成的整个图形为中心对称图形,且四个菱形重叠部分面积为$8\sqrt{3}$,则$a= $2.

答案： 2 [解析]由题意,得$AA_{1}=BB_{1}=B_{1}B_{2}=CC_{1}=C_{2}C_{3}=D_{2}D_{3}=DD_{3}=a,\therefore A_{2}B_{3}=6-a,∠D_{1}A_{2}B_{3}=60^{\circ }$.
连接$B_{3}D_{1}$,
∵四个菱形的重叠部分,即菱形$A_{2}B_{3}CD_{1}$的面积为$8\sqrt {3},\therefore S_{菱形A_{2}B_{3}CD_{1}}=2S_{△A_{2}B_{3}D_{1}}=2×\frac {\sqrt {3}}{4}(6-a)^{2}=8\sqrt {3}$,
解得$a=2$或$a=10$(不合题意,舍去).故$a=2$.