《2025年实验班提优训练九年级数学上册人教版》

1. (2023·沈阳中考)二次函数$y = -(x + 1)^2 + 2$图象的顶点所在的象限是(B).
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限

答案： B

2. (2025·浙江宁波镇海区蛟川书院月考)已知抛物线$y = -(x + 3)^2 + \frac{1}{3}$,下列说法正确的是(D).
A. 开口向上
B. 与$y轴的交点为(0,\frac{1}{3})$
C. 顶点坐标为$(3,\frac{1}{3})$
D. 当$x ＜ -4$时,$y随x$的增大而增大

答案： D[解析]A.a=−1＜0,抛物线开口向下,故选项A不符合题意;B.抛物线与y轴的交点坐标是(0,−$\frac{26}{3}$),故选项B不符合题意;C.顶点坐标为(−3,$\frac{1}{3}$),故选项C不符合题意;D.当x＜−4时,y随x的增大而增大,故选项D符合题意.故选D.

3. (2024·凉山州中考)抛物线$y = \frac{2}{3}(x - 1)^2 + c经过(-2,y_1),(0,y_2),(\frac{5}{2},y_3)$三点,则$y_1,y_2,y_3$的大小关系正确的是(D).
A. $y_1 ＞ y_2 ＞ y_3$
B. $y_2 ＞ y_3 ＞ y_1$
C. $y_3 ＞ y_1 ＞ y_2$
D. $y_1 ＞ y_3 ＞ y_2$

答案： D[解析]
∵抛物线y=$\frac{2}{3}$(x−1)²+c开口向上,对称轴是直线x=1,
∴当x＜1时，y随x的增大而减小.
∵($\frac{5}{2}$,y3)关于直线x=1的对称点是(−$\frac{1}{2}$,y3),且−2＜−$\frac{1}{2}$＜0＜1,
∴y1＞y3＞y2.故选D.

4. 教材P35例3·变式(2025·江苏苏州工业园区期中)将抛物线$y = (x - 1)^2 - 2$,先向上平移3个单位长度,再向左平移2个单位长度,所得新抛物线的函数关系式为y=(x+1)²+1.

答案： y=(x+1)²+1　[解析]将抛物线y=(x−1)²−2,先向上平移3个单位长度,再向左平移2个单位长度,所得新抛物线的函数关系式为y=(x−1+2)²−2+3=(x+1)²+1,即y=(x+1)²+1.

5. 实验班原创 已知抛物线$y = -2(x + h)^2 - k$,当$x \geq 2$时,$y随x$的增大而减小,那么$h$的取值范围是h≥−2.

答案： h≥−2　[解析]
∵y=−2(x+h)²−k,
∴对称轴为直线x=−h.
∵a=−2＜0,
∴抛物线开口向下，
∴在对称轴右侧,y随x的增大而减小.
∵当x≥2时,y随x的增大而减小,
∴−h≤2,解得h≥−2.

6. (2024·滨州中考)将抛物线$y = -x^2$先向右平移1个单位长度,再向上平移2个单位长度,则平移后抛物线的顶点坐标为(1,2).

答案： (1,2)　[解析]将抛物线y=−x²先向右平移1个单位长度，再向上平移2个单位长度后抛物线解析式为y=−(x−1)²+2,
∴平移后抛物线的顶点坐标为(1,2).

7. 教材P36例4·变式 某幢建筑物,从$\frac{20}{3}$米高的窗口A用水管向外喷水,喷的水流呈抛物线(抛物线所在平面与墙面垂直),如图,如果抛物线的最高点M离墙2米,离地面12米,求水流落地点B到墙的距离OB.

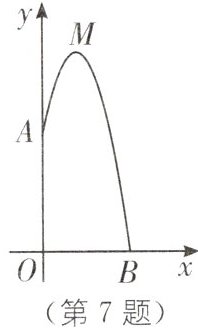
OB为5米.

答案： 设抛物线解析式为y=a(x−2)²+12,把点A(0,$\frac{20}{3}$)代入抛物线解析式,得$\frac{20}{3}$=4a+12,解得a=−$\frac{4}{3}$.故抛物线解析式为y=−$\frac{4}{3}$(x−2)²+12.令y=0,则−$\frac{4}{3}$(x−2)²+12=0,解得x1=−1(舍去),x2=5,即可得OB=5米.故水流落地点B到墙的距离OB为5米.

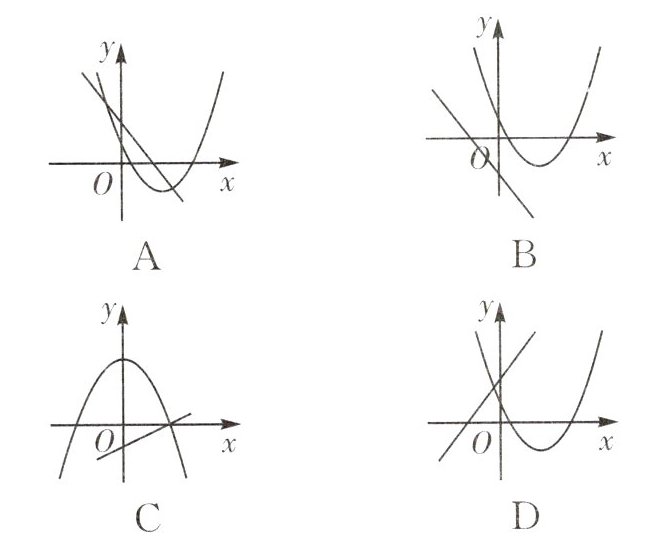
8. (2025·江苏苏州姑苏区振华中学期中)二次函数$y = a(x - 3)^2 + c与一次函数y = cx + a$在同一平面直角坐标系中的大致图象是(A).

答案： A[解析]A.一次函数y=cx+a的图象过第一、二、四象限,a＞0,c＜0,二次函数y=a(x−3)²+c的图象开口向上,顶点为(3,c)在第四象限,a＞0,c＜0,故A正确;B.一次函数y=cx+a的图象与y轴交于负半轴,a＜0,与二次函数y=a(x−3)²+c的图象开口向上,即a＞0相矛盾，故B错误;C.二次函数y=a(x−3)²+c的对称轴为直线x=3,应在y轴右侧,故C错误;D.一次函数y=cx+a的图象过第一、二、三象限,c＞0,与抛物线y=a(x−3)²+c的顶点(3,c)在第四象限，c＜0相矛盾,故D错误.故选A.

9. 已知函数$y = \begin{cases}(x - 1)^2 - 1(x \leq 3),\x - 5)^2 - 1(x ＞ 3),\end{cases}$若使y = k成立的x的值恰好有3个,则k的值为( ).
A. 0
B. 1
C. 2
D. 3

答案：
D[解析]函数y=$\begin{cases}(x - 1)^2 - 1(x \leq 3), \\ (x - 5)^2 - 1(x ＞ 3)\end{cases}$的图象如图，根据图象知道当y=3时,对应成立的x的值恰好有三个，
∴k=3.故选D

解题关键　利用二次函数的图象解决交点问题，关键是把解方程的问题转换为根据函数图象找交点的问题

10. (2025·安徽安庆四中期中)已知一条抛物线的形状与抛物线$y = 2x^2 + 3$形状相同,与另一条抛物线$y = -\frac{1}{2}(x + 1)^2 - 2$的顶点坐标相同,这条抛物线的解析式为y=±2(x+1)²−2.

答案： y=±2(x+1)²−2　[解析]
∵一条抛物线的形状与抛物线y=2x²+3形状相同,
∴a=±2.设抛物线的解析式为y=±2(x−h)²+k,由y=−$\frac{1}{2}$(x+1)²−2可知顶点坐标是(−1,−2),
∴此抛物线顶点坐标是(−1,−2),
∴抛物线的解析式为y=±2(x+1)²−2.