《2025年实验班提优训练九年级数学上册人教版》

7. (重庆渝中区巴蜀中学自主招生)如图,在平行四边形ABCD中,AC是对角线,$∠CAB= 90^{\circ }$,以点A为圆心,以AB的长为半径作$\odot A$,交BC边于点E,交AC于点F,连接DE,且$∠ADE= 30^{\circ },AD= 6$,则阴影部分的面积为____.

答案：
$\frac{9\sqrt{3}}{4} - \frac{3}{4}\pi$ [解析] 如图，连接 $AE$。$\because$ 四边形 $ABCD$ 是平行四边形，$\therefore AD = BC = 6$，$AD // BC$，
$\therefore \angle DAE = \angle AEB$。
$\because AE = AB$，$\therefore \angle AEB = \angle ABC$，
$\therefore \angle DAE = \angle ABC$，
$\therefore \triangle AED \cong \triangle BAC(SAS)$，
$\therefore \angle ACB = \angle ADE = 30^{\circ}$，
$\therefore \angle ABC = 60^{\circ}$，$AB = \frac{1}{2}BC = 3$，
$\therefore AC = \sqrt{BC^2 - AB^2} = 3\sqrt{3}$。$\because AE = AB = 3$，
$\therefore \triangle ABE$ 是等边三角形，$\therefore AE = BE$，$\angle EAB = 60^{\circ}$。
$\because \angle CAB = 90^{\circ}$，$\therefore \angle CAE = 90^{\circ} - \angle EAB = 90^{\circ} - 60^{\circ} = 30^{\circ}$。
$\because \angle ACB = 90^{\circ} - 60^{\circ} = 30^{\circ}$，$\therefore \angle CAE = \angle ACB$，
$\therefore AE = CE$，$\therefore CE = BE$。
$\because S_{\triangle ABC} = \frac{1}{2}AB \cdot AC = \frac{1}{2} \times 3 \times 3\sqrt{3} = \frac{9\sqrt{3}}{2}$，
$\therefore S_{\triangle ACE} = \frac{1}{2}S_{\triangle ABC} = \frac{9\sqrt{3}}{4}$。
$\because \angle CAE = 30^{\circ}$，$AE = 3$，$\therefore S_{扇形AEF} = \frac{30\pi \times 3^2}{360} = \frac{3}{4}\pi$，
$\therefore S_{阴影} = S_{\triangle ACE} - S_{扇形AEF} = \frac{9\sqrt{3}}{4} - \frac{3}{4}\pi$。
知识拓展 求不规则图形面积的方法：
(1) 相加法：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积；
(2) 相减法：这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差；
(3) 直接求法：这种方法是根据已知条件，从整体出发直接求出不规则图形的面积；
(4) 重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形的面积即可。

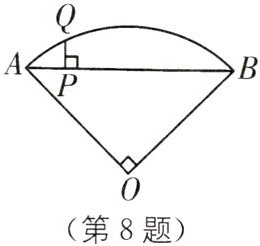
8. (2025·江苏常州溧阳期中)如图,在扇形AOB中,$∠AOB= 90^{\circ }$,点P是AB上一点,$AP= \frac {1}{5}BP= \sqrt {2}$.
(1)求扇形AOB的面积;
(2)过点P作$PQ⊥AB交\widehat {AB}$于点Q,求PQ的长.

答案：

(1) $\because AP = \frac{1}{5}BP = \sqrt{2}$，$\therefore BP = 5\sqrt{2}$，
$\therefore AB = AP + BP = 6\sqrt{2}$。$\because OA = OB$，$\angle AOB = 90^{\circ}$，
$\therefore \triangle OAB$ 是等腰直角三角形，
由勾股定理，得 $AB = \sqrt{OA^2 + OB^2} = \sqrt{2}OA$，
$\therefore \sqrt{2}OA = 6\sqrt{2}$，$\therefore OA = 6$，
$\therefore$ 扇形 $AOB$ 的面积 $= \frac{90\pi \times 6^2}{360} = 9\pi$。
(2) 过点 $O$ 作 $OC \perp AB$ 于点 $C$，作 $OD \perp PQ$ 交 $QP$ 的延长线于点 $D$，连接 $OQ$，如图。
$\because PQ \perp AB$，$OC \perp AB$，$OD \perp PD$，
$\therefore$ 四边形 $OCPD$ 为矩形，
$\therefore OC = DP$，$OD = PC$。
由
(1) 知 $\triangle OAB$ 是等腰直角三角形，
且 $OA = OB = 6$，$AB = 6\sqrt{2}$，$AP = \sqrt{2}$，

$\therefore AC = BC = OC = \frac{1}{2}AB = 3\sqrt{2}$，$OQ = OA = 6$，
$\therefore OD = PC = AC - AP = 3\sqrt{2} - \sqrt{2} = 2\sqrt{2}$，$PD = OC = 3\sqrt{2}$，
在 $Rt\triangle ODQ$ 中，由勾股定理，得 $DQ = \sqrt{OQ^2 - OD^2} = \sqrt{6^2 - (2\sqrt{2})^2} = 2\sqrt{7}$，
$\therefore PQ = DQ - PD = 2\sqrt{7} - 3\sqrt{2}$。

9. 类比思想(2024·江苏连云港灌云期中)[问题提出]比较代数式a与b的大小.
[问题探究]要比较代数式a与b的大小,只要求出它们的差$a-b$,若$a-b＞0$,则$a＞b$;若$a-b= 0$,则$a= b$;若$a-b＜0$,则$a＜b$,反之亦然.
[问题解决]
(1)如图(1),有A,B两种型号的钢板,A型钢板的面积比B型钢板大,制作某产品有两种用料方案,方案1:用4块A型钢板,8块B型钢板;方案2:用3块A型钢板,9块B型钢板.从省料角度考虑,应选哪种方案? 请说明理由.
(2)有A,B两块长方形菜地,A菜地的长为$(a+b)$米,宽为b米,B菜地的长为$(b+2c)$米,宽为$(a-c)$米,试比较两块长方形菜地周长的大小.
(3)如图(2),正方形ABCD的边长为a,以A为圆心、$\frac {3}{4}a$为半径作圆弧.以D为圆心、a为半径作圆弧.若图中阴影部分的面积分别为$S_{1},S_{2}$,请你比较$S_{1}与S_{2}$的大小.

答案：

(1) 设 $A$，$B$ 两种型号的钢板的面积分别是 $a$，$b$，
由题意，得 $a ＞ b$，
根据方案 1：用 $4$ 块 $A$ 型钢板，$8$ 块 $B$ 型钢板，
则总用料面积为 $4a + 8b$，
根据方案 2：用 $3$ 块 $A$ 型钢板，$9$ 块 $B$ 型钢板，
则总用料面积为 $3a + 9b$。
$\because 4a + 8b - (3a + 9b) = a - b ＞ 0$，
常用作差法比较大小
$\therefore$ 方案 2 更加省料，应选方案 2。
(2) 根据题意得出 $A$，$B$ 两块长方形菜地的周长分别为 $2(a + b + b) = 2(a + 2b)$，$2(b + 2c + a - c) = 2(b + c + a)$。
$\because 2(a + 2b) - 2(b + c + a) = 2(b - c)$，
$b$，$c$ 的大小无法确定，需分类讨论
若 $b ＞ c$，则 $b - c ＞ 0$，$A$ 的周长大；
若 $b = c$，则 $b - c = 0$，$A$，$B$ 的周长一样大；
若 $b ＜ c$，则 $b - c ＜ 0$，$B$ 的周长大。
(3) 如图，由题意，得 $S_{扇形AEF} = \frac{1}{4}\pi \cdot (\frac{3}{4}a)^2 = \frac{9}{64}a^2\pi$，$S_{扇形DAC} = \frac{1}{4}\pi a^2$，$S_{正方形ABCD} = a^2$，
根据图形可知 $S_1 - S_2 = S_{扇形AEF} + S_{扇形DAC} - S_{正方形ABCD} = \frac{9}{64}a^2\pi + \frac{1}{4}\pi a^2 - a^2 = a^2(\frac{25}{64}\pi - 1)$。
$\because \frac{25}{64}\pi - 1 ＞ 0$，$\therefore S_1 - S_2 ＞ 0$，$\therefore S_1 ＞ S_2$。

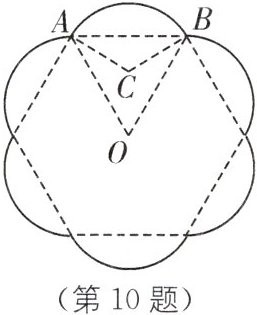
10. (2024·苏州中考)铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,$\widehat {AB}$所在圆的圆心C恰好是$△ABO$的内心,若$AB= 2\sqrt {3}$,则花窗的周长(图中实线部分的长度)= ____.(结果保留π)

答案：
$8\pi$ [解析] 如图，过点 $C$ 作 $CM \perp AB$ 于点 $M$，则 $AM = BM = \frac{1}{2}AB = \sqrt{3}$。
$\because$ 六条等弧所对应的弦构成一个正六边形，中心为点 $O$，
$\therefore \angle AOB = \frac{360^{\circ}}{6} = 60^{\circ}$。
$\because OA = OB$，
$\therefore \triangle AOB$ 是等边三角形，
$\therefore \angle OAB = 60^{\circ}$。
$\because$ 点 $C$ 是 $\triangle AOB$ 的内心，
$\therefore \angle CAB = \angle CAO = \frac{1}{2} \times 60^{\circ} = 30^{\circ}$，$\angle ACB = 2\angle AOB = 120^{\circ}$，
在 $Rt\triangle ACM$ 中，$AM = \sqrt{3}$，$\angle CAM = 30^{\circ}$，
$\therefore CM = \frac{1}{2}AC$，由 $CM^2 + AM^2 = AC^2$，得 $(\frac{1}{2}AC)^2 + 3 = AC^2$，解得 $AC = 2$（负值舍去），
$\therefore \overset{\frown}{AB}$ 的长为 $\frac{120\pi \times 2}{180} = \frac{4}{3}\pi$，
$\therefore$ 花窗的周长为 $\frac{4}{3}\pi \times 6 = 8\pi$。