《2025年实验班提优训练九年级数学上册人教版》

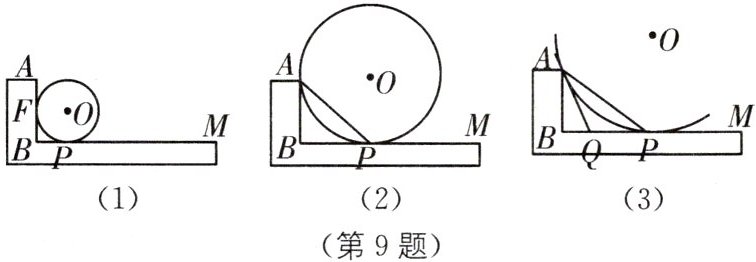
9. 中考新考法 探究最值问题 (2025·江苏宿迁泗阳期中)在数学实验课上,小明取一个角尺($∠ABM= 90^{\circ },AB= 3,BM$可看作无限长)和若干大小不等的圆形纸片(记作$\odot O$)做“停放”实验,当圆形纸片半径较小(圆的半径$r≤3$)时,纸片如图(1)“停放”,其中$\odot O$与线段AB和射线BM分别相切于点F,P,当圆形纸片半径较大(圆的半径$r＞3$)时,纸片如图(2)“停放”,其中$\odot O$经过点A,与射线BM相切于点P.
(1)在图(1)中,若$BP= 2$,求AF的长度.
(2)在图(2)中,设$BP= 4$,则圆的半径$r= $____.
(3)在图(3)中,若$BP＞3$,在点P的左侧取一点Q,使$PQ= m$,连接AQ.
①求当$r= 6$且AQ与$\odot O$相切时m的值及$∠BQA$的度数.
②若$m= 3$,随着r的变化,$\frac {AP}{AQ}$是否有最大值? 如果有,请求出最大值;如果没有,请简要说明理由.

答案：

(1)1 [解析]连接OF,OP,如图
(1).
∵$\odot O$与线段AB和射线BM分别相切于点F,P,
　　　　　　　　　　　　　　　　　
∴∠OFB=∠OPB=90°.
∵∠ABM=90°,
∴四边形BFOP是矩形.
∵OF=OP,
∴四边形BFOP是正方形，
∴BF=BP=2,
∴AF=AB−BF=3−2=1.
(2)如图
(2),连接OA,OP,过点A作AC⊥OP于点C.
∵$\odot O$与射线BM相切于点P,AC⊥OP,
∴∠OPB=∠ACP=90°.
∵∠ABM=90°,
∴四边形ACPB是矩形,
　　　　　　　　　　　　　　　　　
∴AC=BP=4,CP=AB=3.
　设$\odot O$的半径为r,则OA=OP=r,
∴OC=r−3.
　在Rt△AOC中,$AC^{2}+OC^{2}=OA^{2}$,
∴$4^{2}+(r - 3)^{2}=r^{2}$,解得r=$\frac{25}{6}$,
∴$\odot O$的半径为$\frac{25}{6}$.
(3)①如图
(3),连接OA,OP，过点A作AD⊥OP于点D.
∵$\odot O$与射线BM相切于点P,AD⊥OP,
∴∠OPB=∠ADP=90°.
∵∠ABM=90°,
∴四边形ADPB是矩形，
　　　　　　　　　　　　　　　　　
∴AD=BP,DP=AB=3.
∵OA=OP=6,
∴OD=6−3=3,
∴OD=$\frac{1}{2}$OA,
∴∠OAD=30°,AD=$\sqrt{OA^{2}-OD^{2}}$=$\sqrt{6^{2}-3^{2}}$=3$\sqrt{3}$,
∴BP=3$\sqrt{3}$,
∴BQ=3$\sqrt{3}$−m.
∵BM与AQ均与$\odot O$相切，
∴AQ=PQ=m,∠OAQ=∠OPB=90°.
　在Rt△ABQ中,$AB^{2}+BQ^{2}=AQ^{2}$,
∴$3^{2}+(3\sqrt{3}-m)^{2}=m^{2}$,解得m=2$\sqrt{3}$,
∴∠AQP=360°−90°−90°−(90°−30°)=120°,
　②设$\odot O$的半径为r,由①可知，DP=3,
∴OD=r−3.
　在Rt△AOD中,由勾股定理,得
　AD=$\sqrt{OA^{2}-OD^{2}}$=$\sqrt{r^{2}-(r - 3)^{2}}$=$\sqrt{6r - 9}$,
∴BP=AD=$\sqrt{6r - 9}$,
∴BQ=$\sqrt{6r - 9}$−3.
∵∠B=90°,
∴$AQ^{2}=AB^{2}+BQ^{2}=3^{2}+(\sqrt{6r - 9}-3)^{2}=6r + 9 - 6\sqrt{6r - 9}$,$AP^{2}=AB^{2}+BP^{2}=3^{2}+(\sqrt{6r - 9})^{2}=6r$,
∴$(\frac{AP}{AQ})^{2}=\frac{6r}{6r + 9 - 6\sqrt{6r - 9}}$.
　设$\sqrt{6r - 9}=x$,则6r=$x^{2}+9$,
　换元能简化复杂代数式
∴$(\frac{AP}{AQ})^{2}=\frac{x^{2}+9}{x^{2}+9+9 - 6x}=\frac{x^{2}+9}{x^{2}-6x + 18}$,
　令$\frac{x^{2}+9}{x^{2}-6x + 18}=k$,
　整理,得(k−1)$x^{2}-6kx + 18k - 9 = 0$,
　由Δ=$(-6k)^{2}-4(k - 1)(18k - 9)≥0$,
　得$k^{2}-3k + 1≤0$,
　根据二次函数y=$k^{2}-3k + 1$,令y≤0,由图象即可解得$\frac{3-\sqrt{5}}{2}≤k≤\frac{3+\sqrt{5}}{2}$,
∴$(\frac{AP}{AQ})^{2}≤\frac{3+\sqrt{5}}{2}$.
∵$\frac{3+\sqrt{5}}{2}=\frac{6+2\sqrt{5}}{4}=(\frac{\sqrt{5}+1}{2})^{2}$,
∴$\frac{AP}{AQ}≤\frac{\sqrt{5}+1}{2}$,
　即随着r的变化,x与k均随着变化,$\frac{AP}{AQ}$有最大值，最大值是$\frac{\sqrt{5}+1}{2}$.

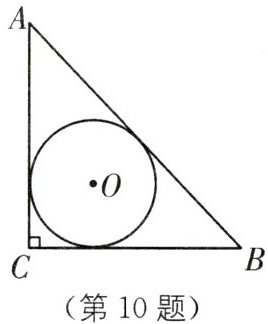
10. 数学文化 勾股容方和勾股容圆 (2024·滨州中考)刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”. 刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式. 如图,$Rt△ABC$中,$∠C= 90^{\circ },AB,BC,CA$的长分别为c,a,b,则可以用含c,a,b的式子表示出$△ABC$的内切圆直径d,下列表达式错误的是( ).

A. $d= a+b-c$
B. $d= \frac {2ab}{a+b+c}$
C. $d= \sqrt {2(c-a)(c-b)}$
D. $d= |(a-b)(c-b)|$

答案：
D [解析]如图,过点O作OE⊥AC于点E,OD⊥BC于点D,OF⊥AB于点F.
　易证四边形OECD是正方形，设OE=OD=OF=r,
　则EC=CD=r.
∵$\odot O$是△ABC的内切圆,AB=c,BC=a,AC=b,
∴AE=AF=b−r,BD=BF=a−r.
∵AF+BF=AB,
　
∴b−r+a−r=c,
　　　　　　　　　　　　　　　　
∴r=$\frac{a+b−c}{2}$,
　
∴d=a+b−c.故选项A正确;
　
∵$S_{△ABC}=S_{△AOC}+S_{△BOC}+S_{△AOB}$,
　
∴$\frac{1}{2}ab=\frac{1}{2}ar+\frac{1}{2}br+cr$,
∴ab=r(a+b+c),
　
∴r=$\frac{ab}{a+b+c}$,即d=$\frac{2ab}{a+b+c}$.故选项B正确;
　　由前面可知d=a+b−c,
　
∴$d^{2}=(a+b−c)^{2}=(a+b)^{2}-2c(a+b)+c^{2}=a^{2}+2ab+b^{2}-2ac-2bc+c^{2}$.
∵$a^{2}+b^{2}=c^{2}$,
　
∴上述式子=$2c^{2}+2ab-2ac-2bc=2(c^{2}+ab-ac-bc)=2[(c^{2}-ac)+b(a-c)]=2(c-a)(c-b)$,
　
∴d=$\sqrt{2(c-a)(c-b)}$,故选项C正确;
　用排除法可知选项D错误.故选D.
一题多解　本题作为选择题，用特殊值法则可快速得到答案,
∵三角形ABC为直角三角形,
∴令a=3,b=4,c=5.选项A:d=a+b−c=2,
选项B:d=$\frac{2ab}{a+b+c}$=2,
选项C:d=$\sqrt{2(c-a)(c-b)}$=2,
选项D:d=|(a-b)(c-b)|=1,
很明显，只有D选项跟其他选项不一致，
∴表达式错误的应是选项D.故选D.