第127页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
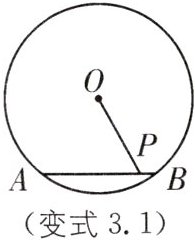
变式3.1 (2025·湖北黄石大冶期中)如图,$\odot O$的半径为10,AB是$\odot O$的弦,$AB= 12$,点P在弦AB上,则线段OP的最小值是____.

答案:
8 [解析]如图,作OH⊥AB于点H,连接OB,由垂径定理,得HA=HB=$\frac{1}{2}$AB=6,
∵OB=10,
∴OH=$\sqrt{BO²−HB²}$=$\sqrt{100−36}$=8,
∴当点P位于点H的位置时,线段OP取最小值8.

8 [解析]如图,作OH⊥AB于点H,连接OB,由垂径定理,得HA=HB=$\frac{1}{2}$AB=6,
∵OB=10,
∴OH=$\sqrt{BO²−HB²}$=$\sqrt{100−36}$=8,
∴当点P位于点H的位置时,线段OP取最小值8.


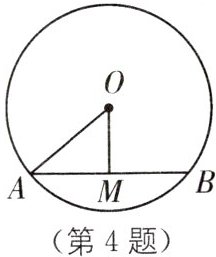
4. 如图,AB是$\odot O$的弦,$OM⊥AB$于点M,若$\odot O$的半径为1,求$OM+AB$的最大值.
(

(
$\sqrt{5}$
)
答案:
设AM=x,
∵OM⊥AB,
∴AB=2x.
在Rt△AOM中,OM=$\sqrt{OA²−AM²}$=$\sqrt{1−x²}$,
设OM+AB=a,即$\sqrt{1−x²}$+2x=a,
∴$\sqrt{1−x²}$=a−2x,
∴1−x²=a²−4ax+4x²,
∴5x²−4ax+a²−1=0,
Δ=(-4a)²−4×5×(a²−1)≥0,即a²≤5,
解得−$\sqrt{5}$≤a≤$\sqrt{5}$,
则a的最大值为$\sqrt{5}$,即OM+AB的最大值为$\sqrt{5}$.
∵OM⊥AB,
∴AB=2x.
在Rt△AOM中,OM=$\sqrt{OA²−AM²}$=$\sqrt{1−x²}$,
设OM+AB=a,即$\sqrt{1−x²}$+2x=a,
∴$\sqrt{1−x²}$=a−2x,
∴1−x²=a²−4ax+4x²,
∴5x²−4ax+a²−1=0,
Δ=(-4a)²−4×5×(a²−1)≥0,即a²≤5,
解得−$\sqrt{5}$≤a≤$\sqrt{5}$,
则a的最大值为$\sqrt{5}$,即OM+AB的最大值为$\sqrt{5}$.
变式4.1 实验班原创 如图,在扇形OAB中,$OA= OB= 2,∠AOB= 60^{\circ }$,点C在弧AB上,$CD⊥AO$,垂足为D,则$△OCD$面积的最大值为(
A. $\frac {1}{2}$
B. $\frac {\sqrt {3}}{2}$
C. 1
D. $\sqrt {3}$
C
).A. $\frac {1}{2}$
B. $\frac {\sqrt {3}}{2}$
C. 1
D. $\sqrt {3}$
答案:
C [解析]
∵OC=2,点C在$\overset{\frown}{AB}$上,CD⊥OA,
∴DC=$\sqrt{OC²−OD²}$=$\sqrt{4−OD²}$,
∴S△OCD=$\frac{1}{2}$OD·$\sqrt{4−OD²}$,
∴S²△OCD=$\frac{1}{4}$OD²·(4−OD²)=−$\frac{1}{4}$OD⁴+OD²=−$\frac{1}{4}$(OD²−2)²+1.
利用配方法和非负数的性质求最值
∵(OD²−2)²≥0,
∴−$\frac{1}{4}$(OD²−2)²≤0,
∴−$\frac{1}{4}$(OD²−2)²+1≤1,
∴当OD²=2,即OD=$\sqrt{2}$时,△OCD的面积最大,最大值为1.故选C;
∵OC=2,点C在$\overset{\frown}{AB}$上,CD⊥OA,
∴DC=$\sqrt{OC²−OD²}$=$\sqrt{4−OD²}$,
∴S△OCD=$\frac{1}{2}$OD·$\sqrt{4−OD²}$,
∴S²△OCD=$\frac{1}{4}$OD²·(4−OD²)=−$\frac{1}{4}$OD⁴+OD²=−$\frac{1}{4}$(OD²−2)²+1.
利用配方法和非负数的性质求最值
∵(OD²−2)²≥0,
∴−$\frac{1}{4}$(OD²−2)²≤0,
∴−$\frac{1}{4}$(OD²−2)²+1≤1,
∴当OD²=2,即OD=$\sqrt{2}$时,△OCD的面积最大,最大值为1.故选C;
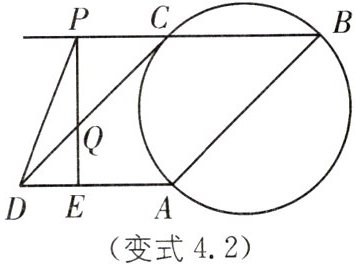
变式4.2 实验班原创 如图,已知$□ ABCD$中,$AD= $$6,∠ADC= 45^{\circ }$,以AB为直径的圆经过点C,Q为线段DC上任一点(与点D,点C不重合),过点Q作直线$PE⊥AD$于E,交射线BC于P,求$△DPQ$的面积的最大值.

答案:
设DE=t,△DPQ的面积为S,连接AC,
∵AB是圆的直径,
∴∠ACB=90°.
∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DAC=90°.
∵∠ADC=45°,
∴AD=AC=6,∠QCP=45°.
∵PE⊥AD,
∴∠AEP=∠ACP=∠DAC=90°,
∴四边形ACPE是矩形,
∴AC=PE=6,∠QED=90°.
∵∠QDE=45°,
∴△DQE是等腰直角三角形,
∴DE=QE=t,
∴PQ=PE−QE=6−t,
∴S=$\frac{1}{2}$PQ·DE=$\frac{1}{2}$t(6−t)=−$\frac{1}{2}$t²+3t=−$\frac{1}{2}$(t−3)²+4.5(0<t<6).
∵(t−3)²≥0,
∴−$\frac{1}{2}$(t−3)²+4.5≤4.5,
∴当t=3时,△DPQ的面积最大为4.5.

设DE=t,△DPQ的面积为S,连接AC,
∵AB是圆的直径,
∴∠ACB=90°.
∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DAC=90°.
∵∠ADC=45°,
∴AD=AC=6,∠QCP=45°.
∵PE⊥AD,
∴∠AEP=∠ACP=∠DAC=90°,
∴四边形ACPE是矩形,
∴AC=PE=6,∠QED=90°.
∵∠QDE=45°,
∴△DQE是等腰直角三角形,
∴DE=QE=t,
∴PQ=PE−QE=6−t,
∴S=$\frac{1}{2}$PQ·DE=$\frac{1}{2}$t(6−t)=−$\frac{1}{2}$t²+3t=−$\frac{1}{2}$(t−3)²+4.5(0<t<6).
∵(t−3)²≥0,
∴−$\frac{1}{2}$(t−3)²+4.5≤4.5,
∴当t=3时,△DPQ的面积最大为4.5.

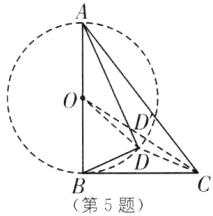
5. (2025·浙江金华永康期中)如图,在$Rt△ABC$中,$∠ABC= 90^{\circ },BC$$=3,AC= 5$,点D是其内部一动点,且$∠DBC= ∠BAD$,则C,D两点的最小距离为(
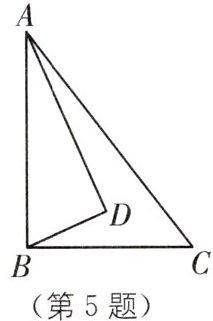
A. 3
B. 4
C. $\sqrt {13}-2$
D. $\sqrt {13}$
C
).
A. 3
B. 4
C. $\sqrt {13}-2$
D. $\sqrt {13}$
答案:
5.C [解析]
∵在Rt△ABC中,∠ABC=90°,BC=3,AC=5,
∴由勾股定理,得AB=$\sqrt{AC²−BC²}$=$\sqrt{5²−3²}$=4,
如图,取AB的中点O,连接OD,
OC交圆于点D',
∵∠DBC=∠BAD,∠DBC+∠ABD=90°,
∴∠BAD+∠ABD=90°,
∴∠ADB=90°,
∴点D在以O为圆心,半径为OA的圆上运动,当O,D,C三点在同一直线上时,CD最短,
此时OD=OD'=OA=2.
在Rt△OCB中,由勾股定理,得OC=$\sqrt{BC²+OB²}$=$\sqrt{3²+2²}$=$\sqrt{13}$,
故CD的最小值为OC−OD'=$\sqrt{13}$−2.故选C.
解后反思 这类问中涉及最值的线段的一个端点是一个动点,且这个动点的运动轨迹是圆或圆弧,画出隐圆,可转化为上述问题中的最值问题.
∵在Rt△ABC中,∠ABC=90°,BC=3,AC=5,
∴由勾股定理,得AB=$\sqrt{AC²−BC²}$=$\sqrt{5²−3²}$=4,
如图,取AB的中点O,连接OD,
OC交圆于点D',
∵∠DBC=∠BAD,∠DBC+∠ABD=90°,
∴∠BAD+∠ABD=90°,
∴∠ADB=90°,
∴点D在以O为圆心,半径为OA的圆上运动,当O,D,C三点在同一直线上时,CD最短,
此时OD=OD'=OA=2.
在Rt△OCB中,由勾股定理,得OC=$\sqrt{BC²+OB²}$=$\sqrt{3²+2²}$=$\sqrt{13}$,
故CD的最小值为OC−OD'=$\sqrt{13}$−2.故选C.
解后反思 这类问中涉及最值的线段的一个端点是一个动点,且这个动点的运动轨迹是圆或圆弧,画出隐圆,可转化为上述问题中的最值问题.
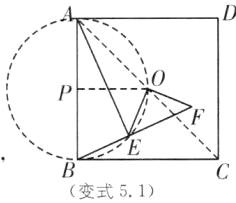
变式5.1 (2025·山东日照东港区北京路中学期中)如图,正方形ABCD的边长为4,点E是平面内一点,连接AE,BE,且$∠AEB= 90^{\circ }$,点O是正方形AB-CD的中心,连接EO,线段EO绕点O逆时针旋转$90^{\circ }$得到线段FO,连接EF,则EF的最大值
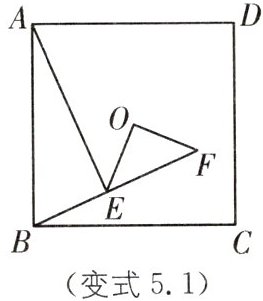
是____

是____
4$\sqrt{2}$
.
答案:
4$\sqrt{2}$ [解析]连接AC,以AB为直径作⊙P,P为圆心,连接OP,如图,
则点P为AB的中点.
∵点E是平面内一点,且∠AEB=90°,
∴点E在⊙P上运动
∵四边形ABCD为正方形,点O为正方形ABCD的中心,边长为4
∴AC过点O,且OA=OC,
AB=BC=4,∠ABC=90°.
∵点P为AB的中点,即PA=PB=$\frac{1}{2}$AB=2,
∴PO为△ABC的中位线,
∴PO=$\frac{1}{2}$BC=2,OP//BC,
∴PO=PA=PB=2.
∴点O在⊙P上.
∵线段EO绕点O逆时针旋转90°得到线段FO,
∴OE=OF,∠EOF=90°,
由勾股定理,得EF=$\sqrt{OE²+OF²}$=$\sqrt{2}$OE,
∴当OE最大时,EF最大.
∵点O,E都在⊙P上,
∴OE为⊙P的弦,
根据圆内最大的弦为直径,得OE的最大值为⊙P的直径,即OE的最大值为4,此时EF的最大值为4$\sqrt{2}$
则点P为AB的中点.
∵点E是平面内一点,且∠AEB=90°,
∴点E在⊙P上运动
∵四边形ABCD为正方形,点O为正方形ABCD的中心,边长为4
∴AC过点O,且OA=OC,
AB=BC=4,∠ABC=90°.
∵点P为AB的中点,即PA=PB=$\frac{1}{2}$AB=2,
∴PO为△ABC的中位线,
∴PO=$\frac{1}{2}$BC=2,OP//BC,
∴PO=PA=PB=2.
∴点O在⊙P上.
∵线段EO绕点O逆时针旋转90°得到线段FO,
∴OE=OF,∠EOF=90°,
由勾股定理,得EF=$\sqrt{OE²+OF²}$=$\sqrt{2}$OE,
∴当OE最大时,EF最大.
∵点O,E都在⊙P上,
∴OE为⊙P的弦,
根据圆内最大的弦为直径,得OE的最大值为⊙P的直径,即OE的最大值为4,此时EF的最大值为4$\sqrt{2}$
变式5.2 在$Rt△ABC$中,$∠A= 90^{\circ },AC= AB= $4,D,E分别是AB,AC的中点,若等腰直角三角形ADE绕点A逆时针旋转,得到等腰直角三角形$AD_{1}E_{1}$,记直线$BD_{1}与CE_{1}$的交点为P,求点P到AB所在直线的距离的最大值.
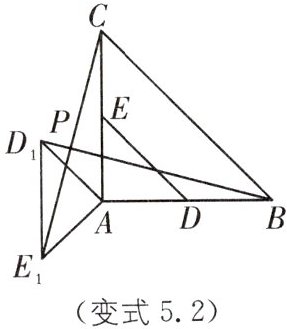

答案:
如图,作PG⊥AB,交AB所在直线于点G,
∵D₁,E₁在以A为圆心,AD为半径的圆上,
当BD₁所在直线与⊙A相切时,直线BD₁与CE₁的交点P到直线AB的距离最大,
易知此时四边形AD₁PE₁是正方形,PD₁=2,
∴在Rt△ABD₁中,BD₁=$\sqrt{AB²−AD²}$=$\sqrt{4²−2²}$=2$\sqrt{3}$,
∠ABP=30°,
则PB=2+2$\sqrt{3}$,
故点P到AB所在直线的距离的最大值PG=1+$\sqrt{3}$.

如图,作PG⊥AB,交AB所在直线于点G,
∵D₁,E₁在以A为圆心,AD为半径的圆上,
当BD₁所在直线与⊙A相切时,直线BD₁与CE₁的交点P到直线AB的距离最大,
易知此时四边形AD₁PE₁是正方形,PD₁=2,
∴在Rt△ABD₁中,BD₁=$\sqrt{AB²−AD²}$=$\sqrt{4²−2²}$=2$\sqrt{3}$,
∠ABP=30°,
则PB=2+2$\sqrt{3}$,
故点P到AB所在直线的距离的最大值PG=1+$\sqrt{3}$.



查看更多完整答案,请扫码查看


