第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
1. 教材P22习题T9·变式 如图,在长为100m,宽为50m的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是$3600m^{2}$,则小路的宽是(
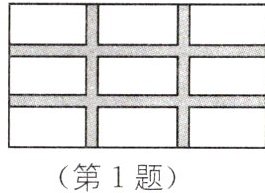
A. 5m
B. 70m
C. 5m或70m
D. 10m
5m
).
A. 5m
B. 70m
C. 5m或70m
D. 10m
答案:
A [解析]设小路的宽是$x$m,则余下的部分可合成长为$(100 - 2x)$m,宽为$(50 - 2x)$m的矩形.根据题意,得$(100 - 2x)(50 - 2x)=3600$,整理,得$x^{2}-75x + 350 = 0$,解得$x_{1}=5,x_{2}=70$(不符合题意,舍去),
∴小路的宽是5m.故选A.
∴小路的宽是5m.故选A.
2. (2024·青岛中考)如图,某小区要在长为16m,宽为12m的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为空地面积的一半,则小路宽为
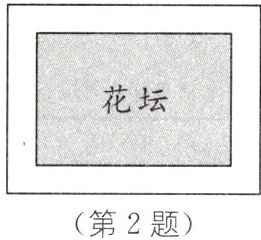
2
m.
答案:
2 [解析]设小路宽为$x$m,根据题意,得$(16 - 2x)(12 - 2x)=\frac{1}{2}\times12\times16$,解得$x = 2$或$x = 12$(舍去),
∴小路宽为2m.
∴小路宽为2m.
3. 教材P20探究3·变式 如图,在长为16m,宽为10m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为整个矩形面积的$\frac {7}{10}$,则道路的宽为
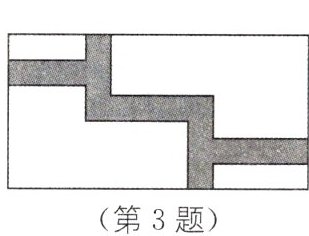
2
m.
答案:
2 [解析]设道路的宽为$x$m,则余下的部分可合成长为$(16 - x)$m,宽为$(10 - x)$m的矩形.依题意,得$(16 - x)(10 - x)=\frac{7}{10}\times16\times10$,整理,得$x^{2}-26x + 48 = 0$,解得$x_{1}=2,x_{2}=24$(舍去).故道路的宽为2m.
4. 为了便于劳动课程的开展,学校打算建一个矩形生态园ABCD(如图),生态园一面靠墙(墙足够长),另外三面用18m的篱笆围成.生态园的面积能否为$40m^{2}$?如果能,请求出AB的长;如果不能,请说明理由.
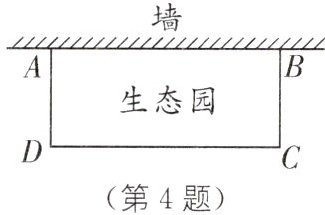
能,AB的长为

能,AB的长为
10m或8m
答案:
生态园的面积能为$40m^{2}$,理由如下:
∵四边形$ABCD$是矩形,
∴$AB = CD,AD = BC$.
设$AB$的长度为$x$m,则$BC$的长度为$\frac{18 - x}{2}$m,
由题意,得$x\cdot\frac{18 - x}{2}=40$,
整理,得$x^{2}-18x + 80 = 0$,解得$x_{1}=10,x_{2}=8$,
∴生态园的面积能为$40m^{2}$,$AB$的长为10m或8m.
知识拓展 本题属于形积问题,常见类型有:①利用勾股定理列一元二次方程,求三角形、矩形的边长;②利用三角形、矩形、菱形、梯形和圆的面积,以及柱体体积公式建立等量关系列一元二次方程.
∵四边形$ABCD$是矩形,
∴$AB = CD,AD = BC$.
设$AB$的长度为$x$m,则$BC$的长度为$\frac{18 - x}{2}$m,
由题意,得$x\cdot\frac{18 - x}{2}=40$,
整理,得$x^{2}-18x + 80 = 0$,解得$x_{1}=10,x_{2}=8$,
∴生态园的面积能为$40m^{2}$,$AB$的长为10m或8m.
知识拓展 本题属于形积问题,常见类型有:①利用勾股定理列一元二次方程,求三角形、矩形的边长;②利用三角形、矩形、菱形、梯形和圆的面积,以及柱体体积公式建立等量关系列一元二次方程.
5. 如图,若将左图正方形剪成四块,恰能拼成右图的矩形,设$a= 1$,则这个正方形的面积为(
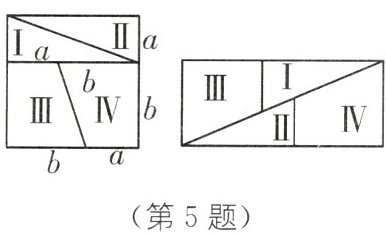
A. $\frac {7+3\sqrt {5}}{2}$
B. $\frac {3+\sqrt {5}}{2}$
C. $\frac {\sqrt {5}+1}{2}$
D. $(1+\sqrt {2})^{2}$
A
).
A. $\frac {7+3\sqrt {5}}{2}$
B. $\frac {3+\sqrt {5}}{2}$
C. $\frac {\sqrt {5}+1}{2}$
D. $(1+\sqrt {2})^{2}$
答案:
A [解析]根据图形和题意,得$(a + b)^{2}=b(a + 2b)$,其中$a = 1$,则方程可化为$(1 + b)^{2}=b(1 + 2b)$,解得$b=\frac{\sqrt{5}+1}{2}$,根据实际意义,负根舍去
所以正方形的面积为$(1+\frac{\sqrt{5}+1}{2})^{2}=\frac{7+3\sqrt{5}}{2}$.故选A.
关键提醒 关键是从两个图形中找到两图形的边长的值,利用面积相等列出等式求方程,解得$b$的值,从而求出正方形的边长,再求面积.
所以正方形的面积为$(1+\frac{\sqrt{5}+1}{2})^{2}=\frac{7+3\sqrt{5}}{2}$.故选A.
关键提醒 关键是从两个图形中找到两图形的边长的值,利用面积相等列出等式求方程,解得$b$的值,从而求出正方形的边长,再求面积.
6. (2025·安徽合肥蜀山区期末)为了节省材料,某农场水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为120米的围网在水库中围成了如图所示的①②③三块矩形区域,且这三块矩形区域的面积都为225平方米,则图中区域①矩形的长a为______
30
米.
答案:
30 [解析]设图中区域①矩形的宽为$x$米,则图中区域②矩形的宽为$2x$米,图中区域①矩形的长$a=\frac{120 - 2x - 3\times2x}{2}=(60 - 4x)$米,根据题意,得$(60 - 4x)x = 225$,整理,得$4x^{2}-60x + 225 = 0$,解得$x_{1}=x_{2}=\frac{15}{2}$,$\therefore a = 60 - 4x = 60 - 4\times\frac{15}{2}=30$(米).
7. 如图,有长为34米的篱笆,一面利用墙(墙的最大可用长度为22米)围成中间隔有一道篱笆的矩形花圃,园主在花圃的前端各设计了两个宽1米的小门,设花圃的宽AB为x米.
(1)若围成的花圃面积为96平方米,求此时的宽AB.
(2)能围成面积为120平方米的花圃吗?若能,请求出x的值;若不能,请说明理由.
(1)∵花圃的宽$AB$为$x$米,
∴花圃的长$AD$为$34 + 2 - 3x=(36 - 3x)$米.
依题意,得$x(34 + 2 - 3x)=96$,解得$x_{1}=4,x_{2}=8$.
当$x = 4$时,$36 - 3x = 24>22$,不合题意,舍去;
当$x = 8$时,$36 - 3x = 12<22$,符合题意.
故此时的宽$AB$为
(2)
依题意,得$x(36 - 3x)=120$,整理,得$x^{2}-12x + 40 = 0$.
∵$\Delta=(-12)^{2}-4×1×40=-16<0$,∴该方程无实数根.
故不能围成面积为120平方米的花圃.
(1)若围成的花圃面积为96平方米,求此时的宽AB.
(2)能围成面积为120平方米的花圃吗?若能,请求出x的值;若不能,请说明理由.
(1)∵花圃的宽$AB$为$x$米,
∴花圃的长$AD$为$34 + 2 - 3x=(36 - 3x)$米.
依题意,得$x(34 + 2 - 3x)=96$,解得$x_{1}=4,x_{2}=8$.
当$x = 4$时,$36 - 3x = 24>22$,不合题意,舍去;
当$x = 8$时,$36 - 3x = 12<22$,符合题意.
故此时的宽$AB$为
8
米.(2)
不能
围成面积为120平方米的花圃.理由如下:依题意,得$x(36 - 3x)=120$,整理,得$x^{2}-12x + 40 = 0$.
∵$\Delta=(-12)^{2}-4×1×40=-16<0$,∴该方程无实数根.
故不能围成面积为120平方米的花圃.
答案:
(1)
∵花圃的宽$AB$为$x$米,
∴花圃的长$AD$为$34 + 2 - 3x=(36 - 3x)$米.
依题意,得$x(34 + 2 - 3x)=96$,解得$x_{1}=4,x_{2}=8$.
当$x = 4$时,$36 - 3x = 24>22$,不合题意,舍去;
当$x = 8$时,$36 - 3x = 12<22$,符合题意.
故此时的宽$AB$为8米.
(2)不能围成面积为120平方米的花圃.理由如下:
依题意,得$x(36 - 3x)=120$,整理,得$x^{2}-12x + 40 = 0$.
∵$\Delta=(-12)^{2}-4\times1\times40=-16<0$,
∴该方程无实数根.
故不能围成面积为120平方米的花圃.
(1)
∵花圃的宽$AB$为$x$米,
∴花圃的长$AD$为$34 + 2 - 3x=(36 - 3x)$米.
依题意,得$x(34 + 2 - 3x)=96$,解得$x_{1}=4,x_{2}=8$.
当$x = 4$时,$36 - 3x = 24>22$,不合题意,舍去;
当$x = 8$时,$36 - 3x = 12<22$,符合题意.
故此时的宽$AB$为8米.
(2)不能围成面积为120平方米的花圃.理由如下:
依题意,得$x(36 - 3x)=120$,整理,得$x^{2}-12x + 40 = 0$.
∵$\Delta=(-12)^{2}-4\times1\times40=-16<0$,
∴该方程无实数根.
故不能围成面积为120平方米的花圃.
查看更多完整答案,请扫码查看


