《2025年实验班提优训练九年级数学上册人教版》

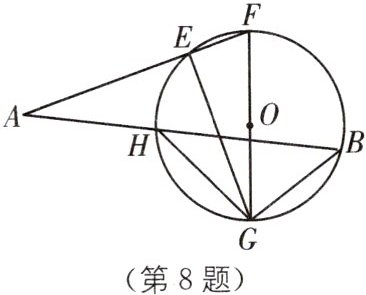
8. (2025·江苏无锡江阴青阳初级中学月考)如图,FG为⊙O的直径$,\overset{\frown}{HF}= \overset{\frown}{HG},E为\overset{\frown}{HF}$上一点,延长FE至点A,使EA= EG,连接HG.
(1)求证:AH= HG;
(2)延长AH交⊙O于点B,连接BG,若$AB= 12\sqrt{2},BG= 6,$求FG的长.

答案：

(1)如图，连接EH、FH，
∵四边形EHGF是⊙O的内接四边形，
∴∠FGH + ∠HEF = 180°。又∠AEH + ∠HEF = 180°，
∴∠FGH = ∠AEH。
∵FG为⊙O的直径，$\overset{\frown}{HF}$ = $\overset{\frown}{HG}$，
∴HF = HG，∠FHG = 90°，
∴∠HFG = ∠HGF = 45°，
∴∠AEH = ∠GEH = 45°。
在△AEH与△GEH中，$\begin{cases}AE = GE,\\∠AEH = ∠GEH,\\EH = EH,\end{cases}$
∴△AEH≌△GEH(SAS)，
∴AH = HG。
(2)如图，过点G作GK⊥AB于点K，
∵FG为⊙O的直径，
∴∠FHG = 90°。
∵$\overset{\frown}{HF}$ = $\overset{\frown}{HG}$，
∴∠HFG = ∠FGH = 45°。
∵$\overset{\frown}{HG}$ = $\overset{\frown}{HG}$，
∴∠HFG = ∠HBG = 45°。
∵BG = 6，GK⊥AB，
∴BK = KG = 3$\sqrt{2}$。
设AH = HG = x，则HK = 12$\sqrt{2}$ - 3$\sqrt{2}$ - x = 9$\sqrt{2}$ - x，
∴在Rt△HKG中，由勾股定理，得$HK^{2}$ + $KG^{2}$ = $HG^{2}$，即(9$\sqrt{2}$ - x)² + (3$\sqrt{2}$)² = x²，解得x = 5$\sqrt{2}$，
∴FG = $\sqrt{2}$HG = 5$\sqrt{2}$×$\sqrt{2}$ = 10。

9. 如图,点A,B,C,D,E在⊙O上顺次排列,已知AB= BC,∠ABD= ∠BCE.
(1)求证:BD= CE;
(2)若直线AE过圆心O,设∠BCE的度数为$α,\overset{\frown}{CD}$的度数为β.
①当β= 60°时,求α的值;
②探索α和β满足的等量关系.
(1)∵AB = BC，∴$\overset{\frown}{AB}$ = $\overset{\frown}{BC}$。∵∠ABD = ∠BCE，
∴$\overset{\frown}{AED}$ = $\overset{\frown}{BAE}$，即$\overset{\frown}{AE}$ + $\overset{\frown}{DE}$ = $\overset{\frown}{AB}$ + $\overset{\frown}{AE}$，
∴$\overset{\frown}{AB}$ = $\overset{\frown}{DE}$，∴$\overset{\frown}{AB}$ = $\overset{\frown}{BC}$ = $\overset{\frown}{DE}$，
∴$\overset{\frown}{BC}$ + $\overset{\frown}{CD}$ = $\overset{\frown}{DE}$ + $\overset{\frown}{CD}$，即$\overset{\frown}{BD}$ = $\overset{\frown}{CE}$，∴BD = CE。
(2)①连接AE，OB。∵$\overset{\frown}{CD}$的度数β = 60°，直线AE过圆心O，
∴$\overset{\frown}{AB}$ = $\overset{\frown}{BC}$ = $\overset{\frown}{DE}$，其度数都等于$\frac{180^{\circ}-60^{\circ}}{3}$ = 40°，
∴∠AOB = 40°。
弧的度数即它所对圆心角的度数
∵点A，B，C，E在⊙O上，
∴四边形ABCE是⊙O的内接四边形，
∴∠BCE + ∠A = 180°，
∴∠BCE = 180° - $\frac{180^{\circ}-40^{\circ}}{2}$ = 180° - 70° = 110°，
即α = 110°。
②6α + β = 720°。理由如下：
∵$\overset{\frown}{CD}$的度数为β，直线AE过圆心O，
∴$\overset{\frown}{AB}$ = $\overset{\frown}{BC}$ = $\overset{\frown}{DE}$，其度数都等于$\frac{180^{\circ}-\beta}{3}$，
∴∠AOB = $\frac{180^{\circ}-\beta}{3}$。
∵四边形ABCE是⊙O的内接四边形，
∴∠BCE + ∠A = 180°，
∴∠BCE = 180° - ∠A = 180° - $\frac{180^{\circ}-∠AOB}{2}$
= 90° + $\frac{1}{2}$∠AOB = 90° + $\frac{1}{2}$×$\frac{180^{\circ}-\beta}{3}$，
化简时注意符号问题
即α = 90° + $\frac{1}{2}$×$\frac{180^{\circ}-\beta}{3}$，∴6α + β = 720°。

答案：
(1)
∵AB = BC，
∴$\overset{\frown}{AB}$ = $\overset{\frown}{BC}$。
∵∠ABD = ∠BCE，
∴$\overset{\frown}{AED}$ = $\overset{\frown}{BAE}$，即$\overset{\frown}{AE}$ + $\overset{\frown}{DE}$ = $\overset{\frown}{AB}$ + $\overset{\frown}{AE}$，
∴$\overset{\frown}{AB}$ = $\overset{\frown}{DE}$，
∴$\overset{\frown}{AB}$ = $\overset{\frown}{BC}$ = $\overset{\frown}{DE}$，
∴$\overset{\frown}{BC}$ + $\overset{\frown}{CD}$ = $\overset{\frown}{DE}$ + $\overset{\frown}{CD}$，即$\overset{\frown}{BD}$ = $\overset{\frown}{CE}$，
∴BD = CE。
(2)①连接AE，OB。
∵$\overset{\frown}{CD}$的度数β = 60°，直线AE过圆心O，
∴$\overset{\frown}{AB}$ = $\overset{\frown}{BC}$ = $\overset{\frown}{DE}$，其度数都等于$\frac{180^{\circ}-60^{\circ}}{3}$ = 40°，
∴∠AOB = 40°。
弧的度数即它所对圆心角的度数
∵点A，B，C，E在⊙O上，
∴四边形ABCE是⊙O的内接四边形，
∴∠BCE + ∠A = 180°，
∴∠BCE = 180° - $\frac{180^{\circ}-40^{\circ}}{2}$ = 180° - 70° = 110°，
即α = 110°。
②6α + β = 720°。理由如下：
∵$\overset{\frown}{CD}$的度数为β，直线AE过圆心O，
∴$\overset{\frown}{AB}$ = $\overset{\frown}{BC}$ = $\overset{\frown}{DE}$，其度数都等于$\frac{180^{\circ}-\beta}{3}$，
∴∠AOB = $\frac{180^{\circ}-\beta}{3}$。
∵四边形ABCE是⊙O的内接四边形，
∴∠BCE + ∠A = 180°，
∴∠BCE = 180° - ∠A = 180° - $\frac{180^{\circ}-∠AOB}{2}$
= 90° + $\frac{1}{2}$∠AOB = 90° + $\frac{1}{2}$×$\frac{180^{\circ}-\beta}{3}$，
化简时注意符号问题
即α = 90° + $\frac{1}{2}$×$\frac{180^{\circ}-\beta}{3}$，
∴6α + β = 720°。

10. 四点共圆模型 (湖北黄冈中学自主招生)如图,四边形ABCD为正方形,⊙O过正方形的顶点A和对角线的交点P,分别交AB,AD于点F,E.
(1)求证:DE= AF;
(2)若⊙O的半径为$\frac{\sqrt{3}}{2},AB= \sqrt{2}+1,求\frac{AE}{ED}$的值.

答案：

(1)连接EP，FP，如图。
∵四边形ABCD为正方形，
∴∠BAD = 90°，∠BPA = 90°，
PA = PB，
∴∠FPE = 90°，
∴∠BPF = ∠APE。
∵∠FBP = ∠PAE = 45°，
∴△BPF≌△APE(ASA)，
∴BF = AE，而AB = AD，
∴DE = AF。
(2)如图，连接EF。
∵∠BAD = 90°，
∴EF为⊙O的直径，
而⊙O的半径为$\frac{\sqrt{3}}{2}$，
∴EF = $\sqrt{3}$，
∴$AF^{2}$ + $AE^{2}$ = $EF^{2}$ = ($\sqrt{3}$)² = 3，
而DE = AF，
∴$DE^{2}$ + $AE^{2}$ = 3①。
∵AD = AE + ED = AB，
∴AE + ED = $\sqrt{2}$ + 1②，
由①②联立起来组成方程组，解得AE = 1，ED = $\sqrt{2}$或AE = $\sqrt{2}$，ED = 1，
∴$\frac{AE}{ED}$ = $\frac{\sqrt{2}}{2}$或$\sqrt{2}$。

11. (2024·浙江中考)如图,在圆内接四边形ABCD中,AD＜AC,∠ADC＜∠BAD,延长AD至点E,使AE= AC,延长BA至点F,连接EF,使∠AFE= ∠ADC.
(1)若∠AFE= 60°,CD为直径,求∠ABD的度数.
(2)求证:
①EF// BC;
②EF= BD.

答案：

(1)
∵CD为直径，
∴∠CAD = 90°。
∵∠AFE = ∠ADC = 60°，
∴∠ACD = 90° - 60° = 30°，
∴∠ABD = ∠ACD = 30°。
(2)①如图，延长AB，
∵四边形ABCD是圆内接四边形，
∴∠ADC + ∠ABC = 180°。
又∠ABC + ∠CBM = 180°，
∴∠CBM = ∠ADC，
∵∠AFE = ∠ADC，
∴∠AFE = ∠CBM，
∴EF//BC。
②如图，过点D作DG//BC交⊙O于点G，连接AG，CG。
∵DG//BC，
∴$\overset{\frown}{BD}$ = $\overset{\frown}{CG}$，
∴BD = CG。
∵四边形ACGD是圆内接四边形，
∴∠GDE = ∠ACG。
∵EF//BC，DG//BC，
∴EF//DG，
∴∠DEF = ∠GDE，
∴∠DEF = ∠ACG。
∵∠AFE = ∠ADC，∠ADC = ∠AGC，
∴∠AFE = ∠AGC。又AE = AC，
∴△AEF≌△ACG(AAS)，
∴EF = CG，
∴EF = BD。