《2025年实验班提优训练九年级数学上册人教版》

11. (2025·山东滨州期中)如图,已知一次函数$y = kx + b的图象与二次函数y = ax^{2}的图象交于点A(1,m)和B(-2,4)$,与$y轴交于点C$。
(1)求两个函数的解析式；
二次函数的解析式为$y=x^{2}$，一次函数的解析式为$y=-x+2$。
(2)求$\triangle AOB$的面积。
3

答案：
(1)把点B(−2,4)代入二次函数y=ax²,得4a=4,解得a=1,
∴二次函数的解析式为y=x².把点A(1,m)代入二次函数解析式,得m=1,把点A(1,1),B(−2,4)代入一次函数y=kx+b,得$\begin{cases}k + b = 1\\-2k + b = 4\end{cases}$,解得$\begin{cases}k = -1\\b = 2\end{cases}$,故一次函数的解析式为y=−x+2.
(2)令x=0,则y=2,
∴一次函数与y轴交于点C(0,2),
∴S△AOB=S△AOC+S△COB=$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×2=3.

12. 方程思想 如图,在平面直角坐标系中,$O$为坐标原点,直线$OA交二次函数y = \frac{1}{4}x^{2}的图象于点A$,$\angle AOB = 90^{\circ}$,点$B$在该二次函数的图象上,设过点$(0,m)$(其中$m ＞ 0$)且平行于$x轴的直线交直线OA于点M$,交直线$OB于点N$,以线段$OM$,$ON为邻边作矩形OMPN$。
(1)若点$A$的横坐标为8。
①用含$m的代数式表示点M$的坐标。
②点$P$能否落在该二次函数的图象上？若能,求出$m$的值；若不能,请说明理由。
(2)当$m = 2$时,若点$P$恰好落在该二次函数的图象上,请直接写出此时满足条件的所有直线$OA$的函数解析式。

答案：

(1)①
∵点A在二次函数y=$\frac{1}{4}$x²的图象上，且点A的横坐标为8.
∴A(8,16),
∴直线OA的解析式为y=2x.
∵点M的纵坐标为m,且点M在直线OA上,
∴点M的坐标为($\frac{1}{2}$m,m).
②能.假设点P能落在该二次函数的图象上，如图，连接OP.
∵∠AOB=90°,直线OA的解析式为y=2x,
∴直线OB的解析式为y=−$\frac{1}{2}$x.
∵点N在直线OB上，点N的纵坐标为m,
∴N(−2m,m),
∴MN的中点的坐标为(−$\frac{3}{4}$m,m).
∵矩形的对角线互相平分，且点O的坐标为(0,0)，
∴P(−$\frac{3}{2}$m,2m).把点P的坐标代入y=$\frac{1}{4}$x²,得$\frac{1}{4}$×(−$\frac{3}{2}$m)²=2m,解得m=$\frac{32}{9}$或m=0(舍去).

(2)①当点A在y轴的右侧时,设A(a,$\frac{1}{4}$a²),a＞0,
∴直线OA的解析式为y=$\frac{1}{4}$ax,
∴M($\frac{8}{a}$,2).
∵∠AOB=90°,即OB⊥OA,
∴直线OB的解析式为y=−$\frac{4}{a}$x,可得N(−$\frac{a}{2}$,2),
∴P($\frac{8}{a}$−$\frac{a}{2}$,4).把点P的坐标代入y=$\frac{1}{4}$x²,得$\frac{1}{4}$×($\frac{8}{a}$−$\frac{a}{2}$)²=4,解得a=4$\sqrt{2}$±4(负值已舍去),
∴直线OA的解析式为y=($\sqrt{2}$±1)x;
②当点A在y轴的左侧时,即为①中点B的位置,
∴直线OA的解析式为y=−$\frac{4}{a}$x=−($\sqrt{2}$±1)x.综上所述,满足条件的直线OA的解析式为y=($\sqrt{2}$±1)x 或y=−($\sqrt{2}$±1)x.

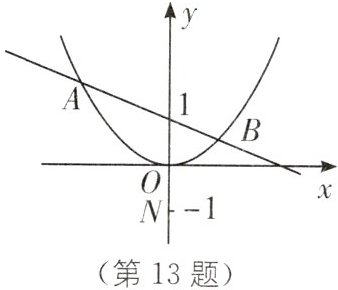
13. (2023·巴中中考)如图,在平面直角坐标系中,直线$y = kx + 1与抛物线y = \frac{1}{4}x^{2}交于A$,$B$两点,设$A(x_{1},y_{1})$,$B(x_{2},y_{2})$,则下列结论正确的个数为(C)。
①$x_{1} \cdot x_{2} = -4$；
②$y_{1} + y_{2} = 4k^{2} + 2$；
③当线段$AB$长取最小值时,则$\triangle AOB$的面积为2；
④若点$N(0,-1)$,则$AN \perp BN$。

A. 1
B. 2
C. 3
D. 4

答案： C　[解析]由题意，联立方程组$\begin{cases}y = kx + 1\\y = \frac{1}{4}x^{2}\end{cases}$,得x₁,x₂满足方程$\frac{1}{4}$x²−kx−1=0,y₁,y₂满足方程y²−(2 + 4k²)y + 1 = 0.依据根与系数的关系,得x₁+x₂=4k,x₁·x₂=−4,y₁+y₂=4k²+2,y₁y₂=1,
∴①②正确;由两点间距离公式,得AB=$\sqrt{(x₁−x₂)²+(y₁−y₂)²}$=$\sqrt{(x₁ + x₂)²−4x₁x₂+(y₁ + y₂)²−4y₁y₂}$=4(k²+1),
∴当k=0时,AB最小值为4,此时S△AOB=$\frac{1}{2}$×1×AB=2,
∴③正确;由题意,得kAN=$\frac{y₁ + 1}{x₁}$,kBN=$\frac{y₂ + 1}{x₂}$,
∴kAN·kBN=$\frac{y₁ + 1}{x₁}$·$\frac{y₂ + 1}{x₂}$=$\frac{(y₁ + 1)(y₂ + 1)}{x₁x₂}$=$\frac{4k² + 2 + 1 + 1}{-4}$=−k²−1,
∴当k=0时,AN⊥BN;当k≠0时,AN与BN不垂直,
∴④错误.故选C.
知识拓展　若直线y₁=k₁x+b₁与直线y₂=k₂x+b₂垂直,则有k₁·k₂=−1.