第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
12. (2025·广东珠海香洲区期中)如图,正方形 $ EFGH $ 的顶点在边长为 2 的正方形 $ ABCD $ 的边上。若设 $ A E = x $,正方形 $ EFGH $ 的面积为 $ y $,求 $ y $ 与 $ x $ 的函数解析式。


答案:
如图所示:
∵四边形ABCD是边长为2的正方形,
∴$∠A = ∠B = 90^{\circ },AB = 2$,
∴$∠1 + ∠2 = 90^{\circ }.$
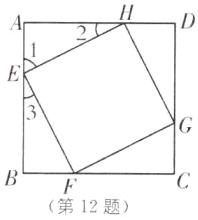
∵四边形EFGH为正方形,
∴$∠HEF = 90^{\circ },EH = EF.$
∴$∠1 + ∠3 = 90^{\circ },\therefore ∠2 = ∠3.$
在$\triangle AHE$和$\triangle BEF$中,
$\left\{\begin{array}{l} ∠A = ∠B\\ ∠2 = ∠3\\ EH = FE\end{array}\right. $
∴$\triangle AHE\cong \triangle BEF(AAS),$
∴$AE = BF = x,AH = BE = 2 - x.$
在$Rt\triangle AHE$中,由勾股定理,得$EH^{2} = AE^{2} + AH^{2} = x^{2} + (2 - x)^{2} = 2x^{2} - 4x + 4$,即$y = 2x^{2} - 4x + 4(0 ≤ x ≤ 2).$
如图所示:
∵四边形ABCD是边长为2的正方形,
∴$∠A = ∠B = 90^{\circ },AB = 2$,
∴$∠1 + ∠2 = 90^{\circ }.$

∵四边形EFGH为正方形,
∴$∠HEF = 90^{\circ },EH = EF.$
∴$∠1 + ∠3 = 90^{\circ },\therefore ∠2 = ∠3.$
在$\triangle AHE$和$\triangle BEF$中,
$\left\{\begin{array}{l} ∠A = ∠B\\ ∠2 = ∠3\\ EH = FE\end{array}\right. $
∴$\triangle AHE\cong \triangle BEF(AAS),$
∴$AE = BF = x,AH = BE = 2 - x.$
在$Rt\triangle AHE$中,由勾股定理,得$EH^{2} = AE^{2} + AH^{2} = x^{2} + (2 - x)^{2} = 2x^{2} - 4x + 4$,即$y = 2x^{2} - 4x + 4(0 ≤ x ≤ 2).$
13. 分类讨论思想 已知在 $ \mathrm { Rt } \triangle A B C $ 中,$ \angle C = 90 ^ { \circ } $,$ A C = B C = 8 \mathrm { cm } $,矩形 $ M N P Q $ 的长和宽分别为 9 cm 和 2 cm,点 $ P $ 和点 $ A $ 重合,$ N P $ 和 $ A C $ 在同一条直线上(如图所示),$ \mathrm { Rt } \triangle A B C $ 不动,矩形 $ M N P Q $ 沿射线 $ N P $ 以每秒 1 cm 的速度向右移动,设移动 $ x ( 0 < x \leq 9 ) \mathrm { s } $ 后,矩形 $ M N - P Q $ 与 $ \triangle A B C $ 重叠部分的面积为 $ y \mathrm { cm } ^ { 2 } $,求 $ y $ 与 $ x $ 之间的函数关系式。


答案:
运动过程中,重叠部分图形的形状在发生改变,重叠部分面积也随之而变化,由此可知题目需进行以下分类讨论:
当$0 < x ≤ 2$时,如图
(1),重叠部分为等腰直角三角形,腰长为x cm,则$y = \frac{1}{2}x^{2}$;
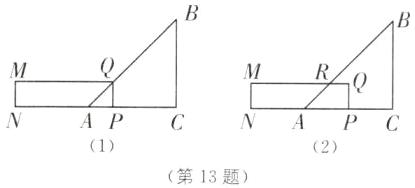
当$2 < x ≤ 8$时,如图
(2),重叠部分为直角梯形,梯形高为2 cm,梯形下底长为x cm,上底长为$(x - 2)cm$,则$y = \frac{1}{2}(x - 2 + x)×2 = 2x - 2$;
当$8 < x ≤ 9$时,如图
(3),重叠部分为直角梯形,梯形高为2 cm,梯形下底长为8 cm,上底长为$8 - 2 = 6(cm)$,则$y = \frac{1}{2}×(6 + 8)×2 = 14.$
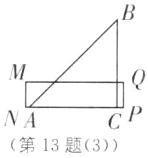
综上所述,$y = \begin{cases} \frac{1}{2}x^{2}(0 < x ≤ 2)\\ 2x - 2(2 < x ≤ 8)\\ 14(8 < x ≤ 9) \end{cases}$
思路引导 根据实际问题确定二次函数关系式时,要读懂题意,建立二次函数的数学模型来解决问题.需要注意的是实例中的函数关系式要根据自变量的取值范围来确定.
运动过程中,重叠部分图形的形状在发生改变,重叠部分面积也随之而变化,由此可知题目需进行以下分类讨论:
当$0 < x ≤ 2$时,如图
(1),重叠部分为等腰直角三角形,腰长为x cm,则$y = \frac{1}{2}x^{2}$;

当$2 < x ≤ 8$时,如图
(2),重叠部分为直角梯形,梯形高为2 cm,梯形下底长为x cm,上底长为$(x - 2)cm$,则$y = \frac{1}{2}(x - 2 + x)×2 = 2x - 2$;
当$8 < x ≤ 9$时,如图
(3),重叠部分为直角梯形,梯形高为2 cm,梯形下底长为8 cm,上底长为$8 - 2 = 6(cm)$,则$y = \frac{1}{2}×(6 + 8)×2 = 14.$

综上所述,$y = \begin{cases} \frac{1}{2}x^{2}(0 < x ≤ 2)\\ 2x - 2(2 < x ≤ 8)\\ 14(8 < x ≤ 9) \end{cases}$
思路引导 根据实际问题确定二次函数关系式时,要读懂题意,建立二次函数的数学模型来解决问题.需要注意的是实例中的函数关系式要根据自变量的取值范围来确定.
14. 某厂生产某种零件,该厂为鼓励销售商订货,提供了如下信息:
①每个零件的成本价为 40 元;
②若订购量不超过 100 个,出厂单价为 60 元;若订购量超过 100 个,每多订 1 个,订购的全部零件的出厂单价就降低 0.02 元;
③实际出厂单价不能低于 51 元。
根据以上信息,解答下列问题:
(1)当一次订购量为____
(2)设一次订购量为 $ x $ 个时,零件的实际出厂单价为 $ P $ 元,写出 $ P $ 与 $ x $ 的函数解析式。
$ P = \begin{cases} 60(0 < x ≤ 100)\\ 62 - \frac{x}{50}(100 < x < 550)\\ 51(x ≥ 550) \end{cases} $
(3)当销售商一次订购 500 个零件时,该厂获得的利润是____
①每个零件的成本价为 40 元;
②若订购量不超过 100 个,出厂单价为 60 元;若订购量超过 100 个,每多订 1 个,订购的全部零件的出厂单价就降低 0.02 元;
③实际出厂单价不能低于 51 元。
根据以上信息,解答下列问题:
(1)当一次订购量为____
550
____个时,每个零件的实际出厂单价恰好降为 51 元。(2)设一次订购量为 $ x $ 个时,零件的实际出厂单价为 $ P $ 元,写出 $ P $ 与 $ x $ 的函数解析式。
$ P = \begin{cases} 60(0 < x ≤ 100)\\ 62 - \frac{x}{50}(100 < x < 550)\\ 51(x ≥ 550) \end{cases} $
(3)当销售商一次订购 500 个零件时,该厂获得的利润是____
6000
____元?如果订购 1000 个,利润又是____11000
____元?(工厂售出一个零件的利润= 实际出厂单价一成本)
答案:
(1)550 [解析]设每个零件的实际出厂单价恰好降为51元时,一次订购量为x个,则$x = 100 + \frac{60 - 51}{0.02} = 550$.故当一次订购量为550个时,每个零件的实际出厂单价恰好降为51元.
(2)当$0 < x ≤ 100$时,$P = 60$;
当$100 < x < 550$时,$P = 60 - 0.02(x - 100) = 62 - \frac{x}{50}$;
当$x ≥ 550$时,$P = 51$.
所以$P = \begin{cases} 60(0 < x ≤ 100)\\ 62 - \frac{x}{50}(100 < x < 550)\\ 51(x ≥ 550) \end{cases}$
分段函数,注意区分不同区间的定义
(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,
$L = (P - 40)x = \begin{cases} 20x(0 < x ≤ 100)\\ 22x - \frac{x^{2}}{50}(100 < x < 550)\\ 11x(x ≥ 550) \end{cases}$
当$x = 500$时,$L = 22×500 - \frac{500^{2}}{50} = 6000$(元);
当$x = 1000$时,$L = 11×1000 = 11000$(元).
故当销售商一次订购500个零件时,该厂获得的利润是6000元;如果订购1000个,利润是11000元.
(1)550 [解析]设每个零件的实际出厂单价恰好降为51元时,一次订购量为x个,则$x = 100 + \frac{60 - 51}{0.02} = 550$.故当一次订购量为550个时,每个零件的实际出厂单价恰好降为51元.
(2)当$0 < x ≤ 100$时,$P = 60$;
当$100 < x < 550$时,$P = 60 - 0.02(x - 100) = 62 - \frac{x}{50}$;
当$x ≥ 550$时,$P = 51$.
所以$P = \begin{cases} 60(0 < x ≤ 100)\\ 62 - \frac{x}{50}(100 < x < 550)\\ 51(x ≥ 550) \end{cases}$
分段函数,注意区分不同区间的定义
(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,
$L = (P - 40)x = \begin{cases} 20x(0 < x ≤ 100)\\ 22x - \frac{x^{2}}{50}(100 < x < 550)\\ 11x(x ≥ 550) \end{cases}$
当$x = 500$时,$L = 22×500 - \frac{500^{2}}{50} = 6000$(元);
当$x = 1000$时,$L = 11×1000 = 11000$(元).
故当销售商一次订购500个零件时,该厂获得的利润是6000元;如果订购1000个,利润是11000元.
查看更多完整答案,请扫码查看


