《2025年实验班提优训练九年级数学上册人教版》

1. 新情境 光盘行动 如图是“光盘行动”的宣传海报,图中餐盘与筷子可看成直线和圆的位置关系是(B).

A. 相切
B. 相交
C. 相离
D. 平行

答案： B

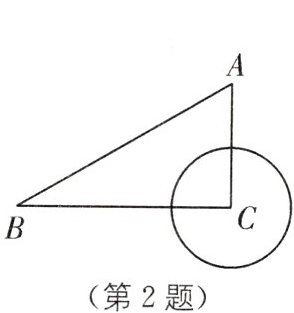
2. (2024·西安雁塔区高新一中一模)如图,在△ABC中,∠C= 90°,∠A= 60°,BC= 4,若⊙C与AB相离,则半径r满足(C).

A. r＞2
B. r＜2
C. 0＜r＜2
D. 0＜r＜2√3

答案： C

3. 教材P96练习·变式 已知⊙O的半径为10 cm,圆心O到直线l的距离为12 cm,则直线l与⊙O的位置关系是相离,有0个公共点.

答案： 相离　0

4. (2024·海南文昌中学期末)在△ABC中,AB= AC= 10,BC= 12,以A为圆心,分别以下列长为半径作圆,请你判定⊙A与直线BC的位置关系.
(1)6;相离(2)8;相切(3)12.相交

答案： 过点A作$AD⊥BC$于点D.
∵$AB=AC=10$，$AD⊥BC$，$BC=12$，
∴$BD=6$，
在$Rt△ABD$中，由勾股定理，得$AD=\sqrt {AB^{2}-BD^{2}}=\sqrt {10^{2}-6^{2}}=8$，
∴圆心A到直线BC的距离d为8。
(1)当$r=6$时，即$d＞r$，则直线BC和$\odot A$相离；
(2)当$r=8$时，即$d=r$，则直线BC和$\odot A$相切；
(3)当$r=12$时，即$d＜r$，则直线BC和$\odot A$相交。

5. 在平面直角坐标系中,以点(-2,3)为圆心,半径为3的圆一定(B).
A. 与x轴相切,与y轴相切
B. 与x轴相切,与y轴相交
C. 与x轴相交,与y轴相切
D. 与x轴相交,与y轴相交

答案： B　[解析]
∵点$(-2,3)$到x轴的距离是3，等于半径，到y轴的距离是2，小于半径，
∴圆与y轴相交，与x轴相切。故选B
归纳总结：判断直线和圆的位置关系有两种方法：一是根据定义，即公共点的个数判断；二是根据圆心到直线的距离d与半径r的大小关系来判断。

6. (2023·宿迁中考)在同一平面内,已知⊙O的半径为2,圆心O到直线l的距离为3,点P为圆上的一个动点,则点P到直线l的最大距离是(B).
A. 2
B. 5
C. 6
D. 8

答案： B

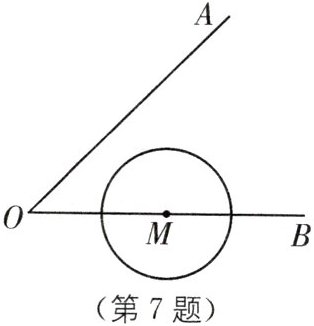
7. 如图,∠AOB= 45°,点M是射线OB上一点,OM= 2,以点M为圆心,r为半径作⊙M,若⊙M与射线OA有两个公共点,则半径r的取值范围是$\sqrt {2}＜r≤2$.

答案： $\sqrt {2}＜r≤2$

8. (2024·江苏扬州宝应期中)在Rt△ABC中,∠C= 90°,AC= 4,BC= 3,若以点C为圆心,r为半径所作的圆与斜边AB只有一个公共点,则r的值是____.

答案：
$3＜r≤4$或$r=2.4$　[解析]如图。
根据勾股定理求得$AB=5$。分两种情况：
(1)圆与AB相切时，即$r=CD=3×4÷5=2.4$；
(2)点B在圆内部，点A在圆上或圆外时，此时$BC＜r≤AC$，即$3＜r≤4$。
故r的值是$3＜r≤4$或$r=2.4$。

易错警示：本题注意两种情况：
(1)圆与AB相切；
(2)点B在圆内部，点A在圆上或圆外。

9. (2023·镇江中考)已知一次函数y= kx+2的图象经过第一、二、四象限,以坐标原点O为圆心,r为半径作⊙O.若对于符合条件的任意实数k,一次函数y= kx+2的图象与⊙O总有两个公共点,则r的最小值为____2.

答案： 2　[解析]在$y=kx+2$中，令$x=0$，则$y=2$，
∴一次函数$y=kx+2$的图象与y轴交于$(0,2)$，
∴一次函数过定点$(0,2)$。当$\odot O$过$(0,2)$时，两者至少有一个交点。
∵一次函数经过第一、二、四象限，
∴此时直线与圆必有两个交点，而当$\odot O$半径小于2时，圆与直线存在相离可能，
∴半径至少为2。故r的最小值为2。

10. (广东深圳中学自主招生)如图,在半径为10的圆中,过距圆心O为20的点A作直线BC,交⊙O于B,C两点,点O到直线BC的距离为6,设AB为x,则$(x+8)^2= ____.$

答案：
364　[解析]如图，连接OA，OC，过点O作$OD⊥BC$于点D。
依题意，得$OA=20$，$OC=10$，$OD=6$。

在$Rt△OCD$中，由勾股定理，得$CD=\sqrt {OC^{2}-OD^{2}}=8$。
∵$OD⊥BC$，
∴$BD=CD=8$。
在$Rt△AOD$中，由勾股定理，得$AD^{2}=OA^{2}-OD^{2}=20^{2}-6^{2}=364$。
∵$AB=x$，$BD=8$，
∴$x + 8 = AB + BD = AD$，
∴$(x + 8)^{2}=364$。