《2025年实验班提优训练九年级数学上册人教版》

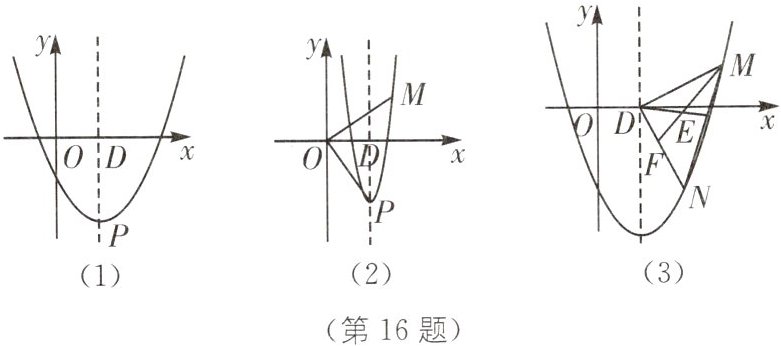
16. 将军饮马模型(2025·广东中山一中期中)[问题背景]已知抛物线$y = a(x - 1)^2 + k$($a,b$为常数,$a ＞ 0$)的顶点为P,对称轴与$x$轴相交于点D,点$M(m,1)$在抛物线上,$m ＞ 1$,O为坐标原点.
[构建联系]
(1)如图(1),当$a = 1$,与$y轴交于点(0,-1)$时,求该抛物线顶点P的坐标;(1,-2)
(2)如图(2),当$OM = OP = \frac{\sqrt{13}}{2}$时,求$a$的值;10
[深入探究]
(3)如图(3),若N是抛物线上的点,且点N在第四象限,$\angle MDN = 90^{\circ},DM = DN$,点E在线段MN上,点F在线段DN上,$NE + NF = \sqrt{2}DM$,当$DE + MF取得最小值为\sqrt{15}$时,求$a$的值.1

答案：
(1)
∵a=1,与y轴交于点(0,−1),
∴−1=(0−1)²+k,解得k=−2,
∴该抛物线的解析式为y=(x−1)²−2,
∴该抛物线顶点P的坐标为(1,−2).
(2)如图
(1),过点M(m,1)作MH⊥x轴，垂足为H,m＞1,则∠MHO=90°,HM=1,OH=m.在Rt△MOH中,由勾股定理,得HM²+OH²=OM²,OM=$\frac{\sqrt{13}}{2}$,
∴1+m²=($\frac{\sqrt{13}}{2}$)²,解得m1=$\frac{3}{2}$,m2=−$\frac{3}{2}$(不合题意，舍去),
∴点M的坐标为($\frac{3}{2}$,1).
∵y=a(x−1)²+k,
∴抛物线的对称轴为直线x=1.
∵对称轴与x轴相交于点D,
∴OD=1,∠ODP=90°.在Rt△OPD中,OP=$\frac{\sqrt{13}}{2}$,由勾股定理,得OD²+PD²=OP²,
∴1+PD²=($\frac{\sqrt{13}}{2}$)²,解得PD=$\frac{3}{2}$或−$\frac{3}{2}$(不合题意，舍去).由a＞0,得该抛物线顶点P的坐标为(1,−$\frac{3}{2}$),
∴该抛物线的解析式为y=a(x−1)²−$\frac{3}{2}$.
∵点M($\frac{3}{2}$,1)在该抛物线上,
∴1=a($\frac{3}{2}$−1)²−$\frac{3}{2}$,解得a=10.
(3)如图
(2),过点M(m,1)作MH⊥x轴,垂足为H,m＞1,则∠MHO=90°,HM=1,OH=m,
∴DH=OH−OD=m−1,
∴在Rt△DMH中,DM²=DH²+HM²=(m−1)²+1.过点N作NK⊥x轴，垂足为K,则∠DKN=90°,
∴∠DNK=90°−∠NDK=∠MDH.在△NDK和△DMH中，$\begin{cases}\angle DKN = \angle MHD, \\ \angle DNK = \angle MDH, \\ DN = DM\end{cases}$,
∴△NDK≌△DMH(AAS),
∴DK=MH=1,NK=DH=m−1,
∴点N的坐标为(2,1−m).在Rt△DMN中,∠DMN=∠DNM=45°,MN²=DM²+DN²=2DM²,即MN=√2DM.根据题意,NE+NF=√2DM,得ME=NF.在△DMN的外部,作∠DNG=∠DME=45°,且NG=DM,连接GM,得∠MNG=∠DNM+∠DNG=90°.在△GNF和△DME中，$\begin{cases}NF = ME, \\ \angle GNF = \angle DME, \\ NG = MD\end{cases}$,
∴△GNF≌△DME(SAS),
∴GF=DE,
∴DE+MF=GF+MF≥GM,当满足条件的点F落在线段GM上时,DE+MF取得最小值,即GM=$\sqrt{15}$.在Rt△GMN中,GM²=NG²+MN²=3DM²,
∴($\sqrt{15}$)²=3DM²,得DM²=5.
∴(m−1)²+1=5,解得m1=3,m2=−1(舍去),
∴点M的坐标为(3,1),点N的坐标为(2,−2).
∵点M(3,1),N(2,−2)都在抛物线y=a(x−1)²+k上,
∴1=a(3−1)²+k,−2=a(2−1)²+k,解得a=1,k=−3.
名师点评　解二次函数与几何知识的综合应用这类问题时，关键是善于利用几何图形的有关性质、定理和二次函数的知识，并注意挖掘题目中的一些隐含条件.解决本题需熟练掌握二次函数的性质、全等三角形的判定和性质等相关知识，灵活运用方程思想、分类讨论思想.

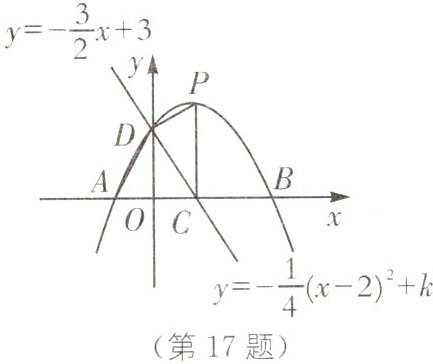
17. (2024·通辽中考)如图,在平面直角坐标系中,直线$y = -\frac{3}{2}x + 3与x$轴,$y$轴分别交于点C,D,抛物线$y = -\frac{1}{4}(x - 2)^2 + k$($k$为常数)经过点D且交$x$轴于A,B两点.
(1)求抛物线表示的函数解析式;
(2)若点P为抛物线的顶点,连接AD,DP,CP.求四边形ACPD的面积.

答案：

(1)在y=−$\frac{3}{2}$x+3中,令x=0,得y=3,
∴D(0,3).
∵抛物线y=−$\frac{1}{4}$(x−2)²+k经过点D(0,3),
∴3=−$\frac{1}{4}$×(0−2)²+k,解得k=4,
∴y=−$\frac{1}{4}$(x−2)²+4=−$\frac{1}{4}$x²+x+3,
∴抛物线表示的函数解析式为y=−$\frac{1}{4}$x²+x+3.
(2)如图,连接OP,

在y=−$\frac{3}{2}$x+3中,令y=0,得x=2,
∴C(2,0),OC=2.在y=−$\frac{1}{4}$x²+x+3中,令y=0,得0=−$\frac{1}{4}$x²+x+3,解得x=6或x=−2,
∴A(−2,0),OA=2.由y=−$\frac{1}{4}$(x−2)²+4可得顶点P坐标为(2,4),
∴S四边形ACPD=SAOD+SPOD+SPOC=$\frac{1}{2}$×2×3+$\frac{1}{2}$×3×2+$\frac{1}{2}$×2×4=3+3+4=10.故四边形ACPD的面积为10.