《2025年实验班提优训练九年级数学上册人教版》

1. (2025·安徽安庆期中)二次函数$y = -x^{2}$的图象的对称轴是(A)。
A. $y$轴
B. $x$轴
C. 直线$x = 1$
D. 直线$x = -1$

答案： A

2. (2024·广东中考)若点$(0,y_{1})$,$(1,y_{2})$,$(2,y_{3})都在二次函数y = x^{2}$的图象上,则(A)。
A. $y_{3} ＞ y_{2} ＞ y_{1}$
B. $y_{2} ＞ y_{1} ＞ y_{3}$
C. $y_{1} ＞ y_{3} ＞ y_{2}$
D. $y_{3} ＞ y_{1} ＞ y_{2}$

答案： A

3. 抛物线$y = 2x^{2}$,$y = -2x^{2}$,共有的性质是(B)。
A. 开口向下
B. 对称轴是$y$轴
C. 都有最低点
D. $y随x$的增大而减小

答案： B[解析]y=2x²和y=−2x²共有的性质是顶点为原点，对称轴为y轴，开口大小相同.故选B.
知识拓展　二次函数y=ax²(a≠0)中a的作用:①a的正负决定抛物线的开口方向和函数的最值,②|a|的大小决定抛物线的开口大小,|a|越大,开口越小;|a|越小,开口越大;|a|相等，说明开口大小相同.

4. 中考新考法 满足结论的条件开放 (2025·浙江湖州期中)已知抛物线$y = (k - 2)x^{2}$的开口向上,写出一个满足条件的$k$值____3(答案不唯一)。

答案： 3(答案不唯一)

5. 如果一个二次函数图象的顶点在$x$轴上,且在$y$轴的右侧部分是上升的,请写出一个符合条件的函数解析式：y=2x²(答案不唯一)。

答案： y=2x²(答案不唯一)

6. 教材P32练习·变式 已知二次函数$y = ax^{2}$,当$x = 3$时,$y = 3$。
(1)求当$x = -2$时,$y$的值；$\frac{4}{3}$
(2)写出它的图象的对称轴、顶点坐标和开口方向。对称轴是y轴，顶点坐标是(0,0)，开口方向是向上。

答案：
(1)把x=3,y=3代入y=ax²,得a×3²=3,解得a=$\frac{1}{3}$,
∴这个二次函数的解析式为y=$\frac{1}{3}$x².当x=−2时,y=$\frac{1}{3}$×(−2)²=$\frac{4}{3}$.
(2)
∵在y=$\frac{1}{3}$x²中,a=$\frac{1}{3}$＞0.
∴它的图象的对称轴是y轴，顶点坐标是(0,0),开口向上.

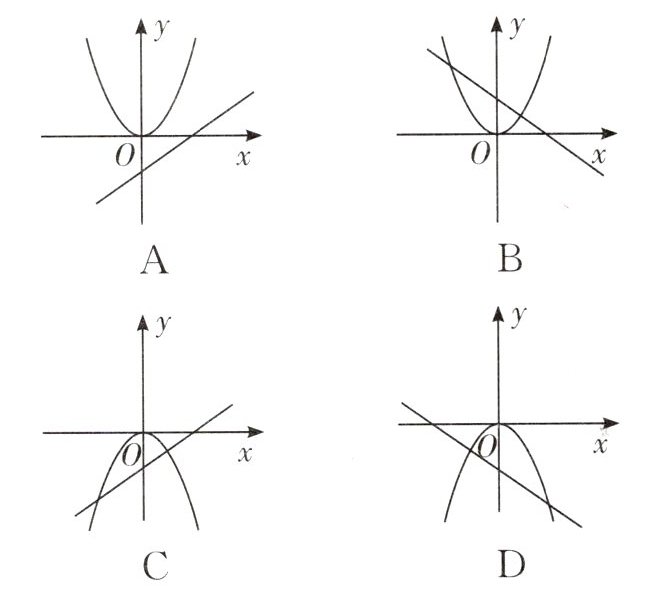
7. 下列图象中,当$ab ＞ 0$时,函数$y = ax^{2}与y = ax + b$的图象是(D)。

答案： D[解析]A.对于直线y=ax+b,得a＞0,b＜0,与ab＞0矛盾,所以A选项错误;B.由抛物线y=ax²开口向上得到a＞0,而由直线y=ax+b经过第一、二、四象限得到a＜0,矛盾,所以B选项错误;C.由抛物线y=ax²开口向下得到a＜0,而由直线y=ax+b经过第一、三、四象限得到a＞0,矛盾,所以C选项错误;D.由抛物线y=ax²开口向下得到a＜0,由直线y=ax+b经过第二、三、四象限得到a＜0,b＜0,符合ab＞0,所以D选项正确.故选D.

8. 中考新考法 新定义问题 设$\max\{x,y\}表示x$,$y$两个数中的最大值,例如“$\max\{1,3\} = 3$,$\max\{-2,0,\frac{1}{4}\} = \frac{1}{4}$”,则关于$x的函数y = \max\{2x,-x - 2,-x^{2}\}$的最小值为____。

答案：
−1　[解析]如图,将y=2x,y=−x−2和y=−x²画在同一个平面直角坐标系中,易得点A的坐标为(−1，−1)，点B的坐标为(0,0).由题意可知，关于x的函数y=max{2x,−x−2,−x²}的图象,即y=2x,y=−x−2和y=−x²在不同范围内的部分图形,即当x≤−1时,y=−x−2,当x=−1时,有最小值,为−1;当−1≤x≤0时,y=−x²,当x=−1时,有最小值,为−1;当x≥0 时,y=2x，当x=0时,有最小值,为0.综上所述,关于x的函数y=max{2x,−x−2,−x²}的最小值为−1.

素养考向　本题通过引入新定义，考查了二次函数和一次函数的性质,学生应具备逻辑推理和判断能力相关素养，运用比较、归纳、演绎、分析与综合等思维方法解决此类新定义问题.

9. 二次函数$y = \frac{2}{3}x^{2}$的图象如图所示,点$A_{0}$位于坐标原点,点$A_{1}$,$A_{2}$,$A_{3}$,…$$,$A_{2025}在y$轴的正半轴上,点$B_{1}$,$B_{2}$,$B_{3}$,…$$,$B_{2025}在二次函数y = \frac{2}{3}x^{2}$位于第一象限的图象上,若$\triangle A_{0}B_{1}A_{1}$,$\triangle A_{1}B_{2}A_{2}$,$\triangle A_{2}B_{3}A_{3}$,…$$,$\triangle A_{2024}B_{2025}A_{2025}$都为等边三角形,则$\triangle A_{2024}B_{2025}A_{2025}$的边长=

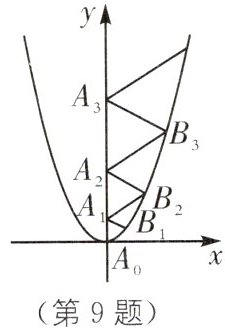
答案：
2025　[解析]如图,分别过$B_{1}$，$B_{2}$，$B_{3}$作y轴的垂线,垂足分别为A，B，C，设$A_{0}A_{1} = a$，$A_{1}A_{2} = b$，$A_{2}A_{3} = c$，则$AB_{1} = \frac{\sqrt{3}}{2}a$，$BB_{2} = \frac{\sqrt{3}}{2}b$，$CB_{3} = \frac{\sqrt{3}}{2}c$.在$\triangle A_{0}B_{1}A_{1}$中，$B_{1}(\frac{\sqrt{3}}{2}a,\frac{a}{2})$，代入$y = \frac{2}{3}x^{2}$中，得$\frac{a}{2} = \frac{2}{3} \cdot (\frac{\sqrt{3}}{2}a)^{2}$，解得$a = 1$或$a = 0$（舍去），即$A_{0}A_{1} = 1$；在$\triangle A_{1}B_{2}A_{2}$中，$B_{2}(\frac{\sqrt{3}}{2}b,1 + \frac{b}{2})$，代入$y = \frac{2}{3}x^{2}$中，得$1 + \frac{b}{2} = \frac{2}{3} \cdot (\frac{\sqrt{3}}{2}b)^{2}$，解得$b = 2$或$b = -1$（舍去），即$A_{1}A_{2} = 2$；在$\triangle A_{2}B_{3}A_{3}$中，$B_{3}(\frac{\sqrt{3}}{2}c,3 + \frac{c}{2})$，代入$y = \frac{2}{3}x^{2}$中，得$3 + \frac{c}{2} = \frac{2}{3} \cdot (\frac{\sqrt{3}}{2}c)^{2}$，解得$c = 3$或$c = -2$（舍去），即$A_{2}A_{3} = 3$，…，由此可得$\triangle A_{2024}B_{2025}A_{2025}$的边长为2025.

10. (2025·江西赣州会昌实验学校月考)已知点$(-2,-3)在二次函数y = ax^{2}$的图象上。
(1)求$a$的值；$-\frac{3}{4}$
(2)若点$(\frac{\sqrt{5} - 1}{2},y_{1})$,$(0,y_{2})$,$(-\frac{\sqrt{2}}{2},y_{3})都在二次函数y = ax^{2}$的图象上,请将$y_{1}$,$y_{2}$,$y_{3}$直接用“$＜$”连接起来。$y_{3}＜y_{1}＜y_{2}$

答案：
(1)
∵点(−2,−3)在二次函数y=ax²的图象上,
∴−3=(−2)²a,解得a=−$\frac{3}{4}$.
(2)由
(1)得y=−$\frac{3}{4}$x²,其图象的对称轴为y轴，离对称轴越远函数值越小.
∵点($\frac{\sqrt{5}−1}{2}$,y₁),(0,y₂),(−$\frac{\sqrt{2}}{2}$,y₃)都在该函数图象上,$\frac{\sqrt{5}−1}{2}$−0=$\frac{\sqrt{5}−1}{2}$＜0−(−$\frac{\sqrt{2}}{2}$)=$\frac{\sqrt{2}}{2}$,
∴y₃＜y₁＜y₂.