《2025年实验班提优训练九年级数学上册人教版》

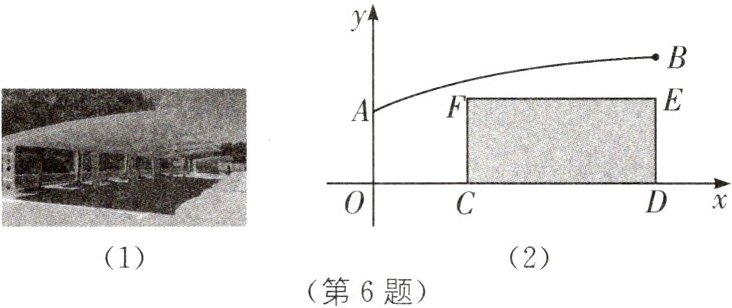
6. (2024·甘肃中考)如图(1)为一汽车停车棚,其棚顶的横截面可以看作是抛物线的一部分,如图(2)是棚顶的竖直高度y(单位:m)与距离停车棚支柱AO的水平距离x(单位:m)近似满足函数关系$y= -0.02x^{2}+0.3x+1.6$的图象,点$B(6,2.68)$在图象上. 若一辆厢式货车需在停车棚下避雨,货车截面看作长$CD= 4m$,高$DE= 1.8m$的矩形,则可判定货车____能____完全停到车棚内(填“能”或“不能”).

答案： 能 [解析]$\because CD = 4m$,$B(6,2.68)$,$\therefore OC = 6 - 4 = 2$.在$y = -0.02x^2 + 0.3x + 1.6$中,当$x = 2$时,$y = -0.02×2^2 + 0.3×2 + 1.6 = 2.12$.
$\because 2.12m ＞ 1.8m$,$\therefore$货车能完全停到车棚内.

7. 中考新考法 方案设计 某加工厂要加工一种抛物线型钢材构件,如图所示,该抛物线型构件的底部宽度$OM= 12$米,顶点P到底部OM的距离为9米. 将该抛物线放入平面直角坐标系中,点M在x轴上. 其内部支架有两个符合要求的设计方案:方案一是“川”字形内部支架(由线段AB,PN,DC构成),点B,N,C在OM上,且$OB= BN= NC= CM$,点A,D在抛物线上,AB,PN,DC均垂直于OM;方案二是“H”形内部支架(由线段$A'B',D'C',EF$构成),点$B',C'$在OM上,且$OB'= B'C'= C'M$,点$A',D'$在抛物线上,$A'B',D'C'$均垂直于OM,E,F分别是$A'B',D'C'$的中点.
(1)求该抛物线对应的函数解析式.$y = -\frac{1}{4}x^2 + 3x$
(2)该加工厂要用某一规格的钢材来加工这种构件,那么哪一个方案的内部支架节省材料? 请说明理由.方案二

答案：
(1)$\because$该抛物线型构件的底部宽度$OM = 12$米,顶点$P$到底部$OM$的距离为$9$米,
$\therefore$顶点$P$的坐标为$P(6,9)$,点$O$的坐标为$O(0,0)$,点$M$的坐标为$M(12,0)$.
设抛物线的函数表达式为$y = a(x - 6)^2 + 9$,将$O(0,0)$代入,得$0 = a×(0 - 6)^2 + 9$,解得$a = -\frac{1}{4}$,$\therefore$该抛物线的函数表达式为$y = -\frac{1}{4}(x - 6)^2 + 9$,即$y = -\frac{1}{4}x^2 + 3x$.
(2)方案二的内部支架节省材料.理由如下:
方案一:$\because OB = BN = NC = CM$,$OM = 12$米,
$\therefore OB = 3$米,$OC = 9$米.
当$x = 3$时,$y = -\frac{1}{4}×(3 - 6)^2 + 9 = \frac{27}{4}$,即$AB = \frac{27}{4}$米,
当$x = 9$时,$y = -\frac{1}{4}×(9 - 6)^2 + 9 = \frac{27}{4}$,即$CD = \frac{27}{4}$米,
$\therefore$方案一内部支架材料长度为$AB + NP + CD = \frac{27}{4} + 9 + \frac{27}{4} = \frac{45}{2}$(米).
方案二:$\because OB' = B'C' = C'M$,$OM = 12$米,
$\therefore OB' = 4$米,$OC' = 8$米,$EF = B'C' = 4$米,
当$x = 4$时,$y = -\frac{1}{4}×(4 - 6)^2 + 9 = 8$,即$A'B' = 8$米,
当$x = 8$时,$y = -\frac{1}{4}×(8 - 6)^2 + 9 = 8$,即$C'D' = 8$米,
$\therefore$方案二内部支架材料长度为$A'B' + EF + C'D' = 8 + 4 + 8 = 20$(米).$\because \frac{45}{2} ＞ 20$,$\therefore$方案二的内部支架节省材料.

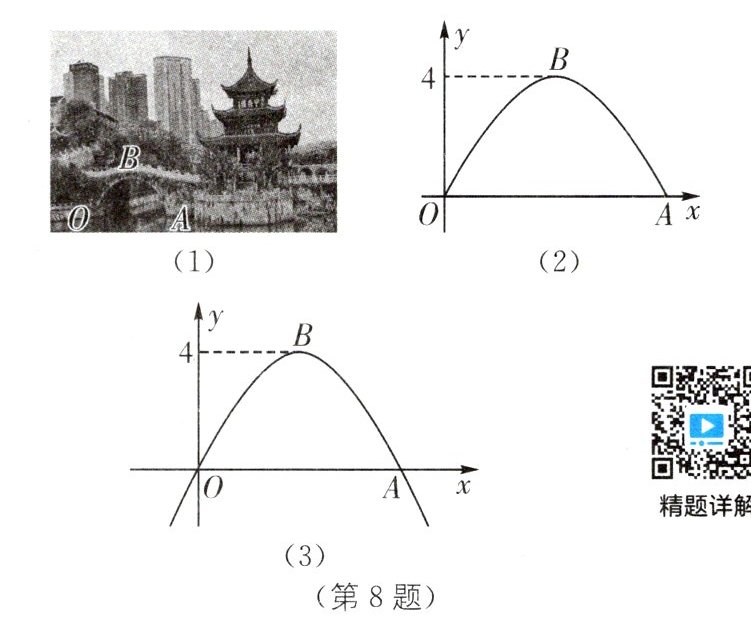
8. 传统文化 甲秀楼 甲秀楼是贵阳的地标建筑,建于明万历年间,已有400多年历史. 如图(1),甲秀楼的桥拱截面OBA可视为抛物线的一部分,在某一时刻,桥拱内的水面宽$OA= 8m$,桥拱顶点B到水面的距离是4m.
(1)按如图(2)所示建立平面直角坐标系,求桥拱部分抛物线对应的函数解析式.
(2)一只宽为1.2m的打捞船径直向桥驶来,当船驶到桥拱下方且距点O0.4m时,桥下水位刚好在OA处,有一名身高1.68m的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱? 请说明理由(假设船底与水面齐平).
(3)如图(3),桥拱所在的函数图象是抛物线$y= ax^{2}+bx+c(a≠0)$,该抛物线在x轴下方部分与桥拱OBA在平静水面中的倒影组成一个新函数图象. 将新函数图象向右平移$m(m＞0)$个单位长度,平移后的函数图象在$8≤x≤9$时,y的值随x值的增大而减小,结合函数图象,求m的取值范围.

答案：

(1)由题意,得水面宽$OA$是$8m$,桥拱顶点$B$到水面的距离是$4m$,结合函数图象可知,顶点$B(4,4)$,点$O(0,0)$,设桥拱部分抛物线的函数表达式为$y = a(x - 4)^2 + 4$,
将点$O(0,0)$代入,得$0 = 16a + 4$,解得$a = -\frac{1}{4}$,
$\therefore$桥拱部分抛物线的函数表达式为$y = -\frac{1}{4}(x - 4)^2 + 4$,即$y = -\frac{1}{4}x^2 + 2x(0 \leq x \leq 8)$.
(2)工人的头顶不会触碰到桥拱.理由如下:
$\because$打捞船距点$O 0.4m$,打捞船宽$1.2m$,工人直立在打捞船中间,$\therefore$工人到点$O$的距离为$0.4 + \frac{1}{2}×1.2 = 1(m)$,将$x = 1$代入$y = -\frac{1}{4}x^2 + 2x$,得$y = \frac{7}{4} = 1.75$.
$\because 1.75m ＞ 1.68m$,$\therefore$此时工人的头顶不会触碰到桥拱.
(3)抛物线$y = -\frac{1}{4}x^2 + 2x$在$x$轴上方的部分与桥拱在平静水面中的倒影关于$x$轴成轴对称.如图
(1),新函数图象的对称轴也是直线$x = 4$,此时,当$0 \leq x \leq 4$或$x \geq 8$时,$y$的值随$x$值的增大而减小.

将新函数图象向右平移$m$个单位长度,可得平移后的函数图象,如图
(2).
$\because$平移不改变图形的形状和大小,
$\therefore$平移后函数图象的对称轴是直线$x = 4 + m$,$\therefore$当$m \leq x \leq 4 + m$或$x \geq 8 + m$时,$y$的值随$x$值的增大而减小.
$\because$当$8 \leq x \leq 9$时,$y$的值随$x$值的增大而减小,
$\therefore$结合函数图象,得$m$的取值范围:
①$m \leq 8$且$4 + m \geq 9$,解得$5 \leq m \leq 8$;
②$8 + m \leq 8$,解得$m \leq 0$.
由题意,知$m ＞ 0$,$\therefore m \leq 0$不符合题意,舍去.
综上所述,$m$的取值范围是$5 \leq m \leq 8$.