第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
1. (2025·安徽淮北期末)如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面上升$\frac {3}{2}m$时,水面的宽度为(
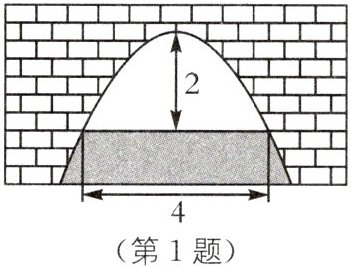
A. $2\sqrt {3}m$
B. $2\sqrt {2}m$
C. 2m
D. $\frac {\sqrt {2}}{2}m$
C
).
A. $2\sqrt {3}m$
B. $2\sqrt {2}m$
C. 2m
D. $\frac {\sqrt {2}}{2}m$
答案:
C
2. 新情境 构建函数模型解决实际问题 (2023·滨州中考)某广场要建一个圆形喷水池,计划在池中心位置竖直安装一根顶部带有喷水头的水管,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心的水平距离也为3m,那么水管的设计高度应为____.
答案:
$\frac{9}{4}$m [解析]如图,建立平面直角坐标系.由题意,知点$(1,3)$是抛物线的顶点,
∴设这段抛物线的解析式为$y = a(x - 1)^2 + 3$.
∵该抛物线过点$(3,0)$,$\therefore 0 = a(3 - 1)^2 + 3$,解得$a = -\frac{3}{4}$,$\therefore y = -\frac{3}{4}(x - 1)^2 + 3$.
∵当$x = 0$时,$y = -\frac{3}{4}×(0 - 1)^2 + 3 = -\frac{3}{4} + 3 = \frac{9}{4}$,
∴水管的设计高度应为$\frac{9}{4}$m.

$\frac{9}{4}$m [解析]如图,建立平面直角坐标系.由题意,知点$(1,3)$是抛物线的顶点,
∴设这段抛物线的解析式为$y = a(x - 1)^2 + 3$.
∵该抛物线过点$(3,0)$,$\therefore 0 = a(3 - 1)^2 + 3$,解得$a = -\frac{3}{4}$,$\therefore y = -\frac{3}{4}(x - 1)^2 + 3$.
∵当$x = 0$时,$y = -\frac{3}{4}×(0 - 1)^2 + 3 = -\frac{3}{4} + 3 = \frac{9}{4}$,
∴水管的设计高度应为$\frac{9}{4}$m.

3. 新情境 发射水火箭 (2024·兰州中考)在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图(1)是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线. 为了解水火箭的相关性能,同学们进一步展开研究. 如图(2)建立平面直角坐标系. 水火箭发射后落在水平地面A处. 科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面OA的竖直高度y(m)与离发射点O的水平距离x(m)的几组关系数据
如下:
(1)根据表格,请确定抛物线的表达式;
(2)请计算当水火箭飞行至离发射点O的水平距离为5m时,水火箭距离地面的竖直高度为
(1)由题意,得抛物线的对称轴是直线$x = \frac{10 + 20}{2} = 15$,
∴抛物线的顶点为$(15,9)$,
∴可设抛物线的表达式为$y = a(x - 15)^2 + 9$.
又抛物线过$(10,8)$,$\therefore 25a = -1$,解得$a = -\frac{1}{25}$,
$\therefore$抛物线的表达式为
(2)由(1),得$y = -\frac{1}{25}(x - 15)^2 + 9$,
令$x = 5$,则$y = -\frac{1}{25}×(5 - 15)^2 + 9 = 5$.
故水火箭距离地面的竖直高度为$5m$.
如下:
(1)根据表格,请确定抛物线的表达式;
(2)请计算当水火箭飞行至离发射点O的水平距离为5m时,水火箭距离地面的竖直高度为
5
m.(1)由题意,得抛物线的对称轴是直线$x = \frac{10 + 20}{2} = 15$,
∴抛物线的顶点为$(15,9)$,
∴可设抛物线的表达式为$y = a(x - 15)^2 + 9$.
又抛物线过$(10,8)$,$\therefore 25a = -1$,解得$a = -\frac{1}{25}$,
$\therefore$抛物线的表达式为
$y = -\frac{1}{25}(x - 15)^2 + 9$
.(2)由(1),得$y = -\frac{1}{25}(x - 15)^2 + 9$,
令$x = 5$,则$y = -\frac{1}{25}×(5 - 15)^2 + 9 = 5$.
故水火箭距离地面的竖直高度为$5m$.
答案:
(1)由题意,得抛物线的对称轴是直线$x = \frac{10 + 20}{2} = 15$,
∴抛物线的顶点为$(15,9)$,
∴可设抛物线的表达式为$y = a(x - 15)^2 + 9$.
又抛物线过$(10,8)$,$\therefore 25a = -1$,解得$a = -\frac{1}{25}$,
$\therefore$抛物线的表达式为$y = -\frac{1}{25}(x - 15)^2 + 9$.
(2)由
(1),得$y = -\frac{1}{25}(x - 15)^2 + 9$,
令$x = 5$,则$y = -\frac{1}{25}×(5 - 15)^2 + 9 = 5$.
故水火箭距离地面的竖直高度为$5m$.
(1)由题意,得抛物线的对称轴是直线$x = \frac{10 + 20}{2} = 15$,
∴抛物线的顶点为$(15,9)$,
∴可设抛物线的表达式为$y = a(x - 15)^2 + 9$.
又抛物线过$(10,8)$,$\therefore 25a = -1$,解得$a = -\frac{1}{25}$,
$\therefore$抛物线的表达式为$y = -\frac{1}{25}(x - 15)^2 + 9$.
(2)由
(1),得$y = -\frac{1}{25}(x - 15)^2 + 9$,
令$x = 5$,则$y = -\frac{1}{25}×(5 - 15)^2 + 9 = 5$.
故水火箭距离地面的竖直高度为$5m$.
4. (2025·山西忻州期中)如图,壮壮同学投掷实心球,出手(点P处)的高度OP是$\frac {7}{4}m$,出手后实心球沿一段抛物线运行,到达最高点时,水平距离是5m,高度是4m. 若实心球落地点为M,则$OM= $
$\frac{35}{3}$
m.
答案:
$\frac{35}{3}$ [解析]以$OM$所在直线为$x$轴,$OP$所在直线为$y$轴,建立平面直角坐标系.设抛物线解析式为$y = a(x - 5)^2 + 4$,把点$(0,\frac{7}{4})$代入,得$25a + 4 = \frac{7}{4}$,解得$a = -\frac{9}{100}$,$\therefore y = -\frac{9}{100}(x - 5)^2 + 4$.
当$y = 0$时,$-\frac{9}{100}(x - 5)^2 + 4 = 0$,解得$x_1 = -\frac{5}{3}$(负值,舍去),$x_2 = \frac{35}{3}$,即此次实心球被推出的水平距离$OM$为$\frac{35}{3}m$.
当$y = 0$时,$-\frac{9}{100}(x - 5)^2 + 4 = 0$,解得$x_1 = -\frac{5}{3}$(负值,舍去),$x_2 = \frac{35}{3}$,即此次实心球被推出的水平距离$OM$为$\frac{35}{3}m$.
5. 某城市规划修建一座观光人行桥,此工程由桥梁工程与桥上拱形工程组成,桥上拱形工程包含三组完全相同的拱形,观光人行桥从正面看过去如图所示,已知桥面上三组拱桥都为抛物线$y= -\frac {1}{16}(x-k)^{2}+t$的一部分,拱高(抛物线最高点到桥面AB的距离)都为16米,三条抛物线依次与桥面AB相交于点A,C,D,B,则桥长$AB= $____米.
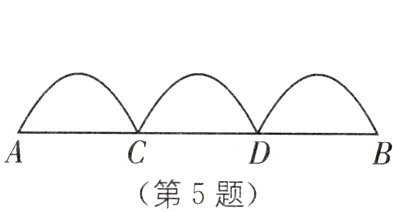

答案:
96 [解析]如图,以线段$AC$的中垂线为$y$轴,直线$AB$为$x$轴,建立平面直角坐标系,

则抛物线$AC$的顶点坐标为$(0,16)$,所以抛物线解析式为$y = -\frac{1}{16}x^2 + 16$.当$y = 0$时,$x_1 = 16$,$x_2 = -16$,
$\therefore$点$A$的坐标为$(-16,0)$,点$C$的坐标为$(16,0)$,
$\therefore AC = 16 - (-16) = 16 + 16 = 32$(米),$\therefore AB = 3AC = 96$米,即桥长$AB$为$96$米.
归纳总结:利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.
96 [解析]如图,以线段$AC$的中垂线为$y$轴,直线$AB$为$x$轴,建立平面直角坐标系,

则抛物线$AC$的顶点坐标为$(0,16)$,所以抛物线解析式为$y = -\frac{1}{16}x^2 + 16$.当$y = 0$时,$x_1 = 16$,$x_2 = -16$,
$\therefore$点$A$的坐标为$(-16,0)$,点$C$的坐标为$(16,0)$,
$\therefore AC = 16 - (-16) = 16 + 16 = 32$(米),$\therefore AB = 3AC = 96$米,即桥长$AB$为$96$米.
归纳总结:利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.
查看更多完整答案,请扫码查看


