第132页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
1. (2025·北京大学附中期中)如图,北京隆福寺毗卢殿明间藻井现藏于北京古代建筑博物馆中,其设计独特,由正八边形、菱形和圆形组合而成.中间雕着一条栩栩如生的盘龙,由整块金丝楠木精雕细琢而成,细节之处彰显匠人技艺.其中正八边形一个内角大小为(

A. $108^{\circ}$
B. $120^{\circ}$
C. $135^{\circ}$
D. $150^{\circ}$
C
).
A. $108^{\circ}$
B. $120^{\circ}$
C. $135^{\circ}$
D. $150^{\circ}$
答案:
C
2. 传统文化 古钱币 如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为 $3:1$,则圆的面积约为正方形面积的(

A. 27倍
B. 14倍
C. 9倍
D. 3倍
B
).
A. 27倍
B. 14倍
C. 9倍
D. 3倍
答案:
B
3. 教材P108习题T5·变式 如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度 $b = 3cm$,则螺帽边长 $a= $
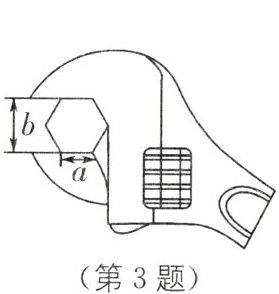
$\sqrt{3}$
$cm$.
答案:
$\sqrt{3}$
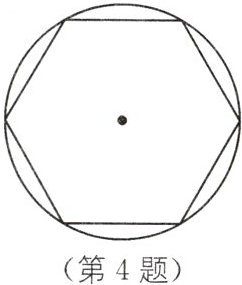
4. 某中学在校园里建了一个读书亭.如图,它的地基是半径为 $6m$ 的正六边形.
(1)地基的周长是多少?
(2)地基的面积是多少?
(1)地基的周长是多少?
(2)地基的面积是多少?

答案:
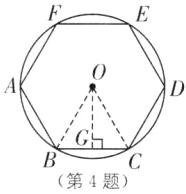
(1)如图,连接OB,OC.
∵六边形ABCDEF是正六边形,
∴$∠BOC=\frac{360^{\circ}}{6}=60^{\circ}$,
∴$△OBC$是等边三角形,
∴$BC=OB=6m$,
∴正六边形ABCDEF的周长$=6×6=36(m)$.
(2)如图,过点O作$OG⊥BC$于点G.
∵$△OBC$是等边三角形,$OB=6m$,
∴$∠BOG=\frac{1}{2}∠BOC=30^{\circ}$,$∴BG=\frac{1}{2}OB=3m$,
∴$OG=\sqrt{OB^{2}-BG^{2}}=3\sqrt{3}m$,
∴$S_{△OBC}=\frac{1}{2}BC\cdot OG=\frac{1}{2}×6×3\sqrt{3}=9\sqrt{3}(m^{2})$,
∴$S_{六边形ABCDEF}=6S_{△OBC}=6×9\sqrt{3}=54\sqrt{3}(m^{2})$.
(1)如图,连接OB,OC.
∵六边形ABCDEF是正六边形,
∴$∠BOC=\frac{360^{\circ}}{6}=60^{\circ}$,

∴$△OBC$是等边三角形,
∴$BC=OB=6m$,
∴正六边形ABCDEF的周长$=6×6=36(m)$.
(2)如图,过点O作$OG⊥BC$于点G.
∵$△OBC$是等边三角形,$OB=6m$,
∴$∠BOG=\frac{1}{2}∠BOC=30^{\circ}$,$∴BG=\frac{1}{2}OB=3m$,
∴$OG=\sqrt{OB^{2}-BG^{2}}=3\sqrt{3}m$,
∴$S_{△OBC}=\frac{1}{2}BC\cdot OG=\frac{1}{2}×6×3\sqrt{3}=9\sqrt{3}(m^{2})$,
∴$S_{六边形ABCDEF}=6S_{△OBC}=6×9\sqrt{3}=54\sqrt{3}(m^{2})$.
5. 新情境 蜂巢结构 (2023·山西中考)蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点 $P,Q,M$ 均为正六边形的顶点.若点 $P,Q$ 的坐标分别为 $(-2\sqrt{3},3),(0,-3)$,则点 $M$ 的坐标为(
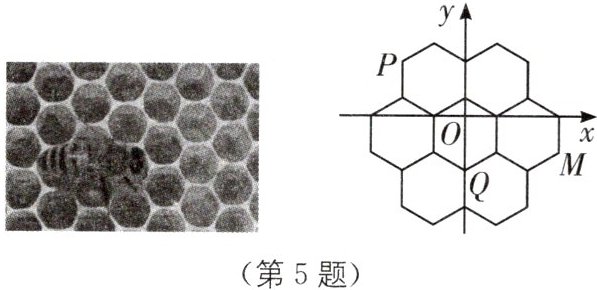
A. $(3\sqrt{3},-2)$
B. $(3\sqrt{3},2)$
C. $(2,-3\sqrt{3})$
D. $(-2,-3\sqrt{3})$
A
).
A. $(3\sqrt{3},-2)$
B. $(3\sqrt{3},2)$
C. $(2,-3\sqrt{3})$
D. $(-2,-3\sqrt{3})$
答案:
A
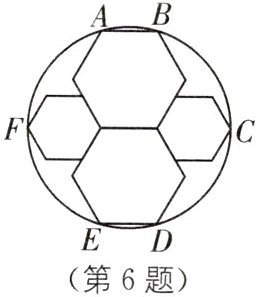
6. 已知四个正六边形如图摆放在圆中,顶点 $A,B,C,D,E,F$ 在圆上.若两个大正六边形的边长均为2,则小正六边形的边长是( ).
A. $3-\sqrt{3}$
B. $\frac{2\sqrt{3}-1}{2}$
C. $\frac{\sqrt{3}+1}{2}$
D. $\frac{\sqrt{13}-1}{2}$

A. $3-\sqrt{3}$
B. $\frac{2\sqrt{3}-1}{2}$
C. $\frac{\sqrt{3}+1}{2}$
D. $\frac{\sqrt{13}-1}{2}$
答案:
D [解析]如图,连接AD交PM于点O,则点O是圆心,过点O作$ON⊥DE$于点N,连接MF,取MF的中点G,连接GH,GQ,
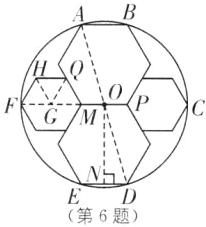
由对称性可知$OM=OP=EN=DN=1$.
由正六边形的性质,得$ON=2\sqrt{3}$,
∴$OD=\sqrt{DN^{2}+ON^{2}}=\sqrt{13}=OF$.
∴$MF=\sqrt{13}-1$.
由正六边形的性质,知$△GFH,△GHQ,△GQM$都是正三角形,$∴FH=\frac{1}{2}MF=\frac{\sqrt{13}-1}{2}$.故选D.
D [解析]如图,连接AD交PM于点O,则点O是圆心,过点O作$ON⊥DE$于点N,连接MF,取MF的中点G,连接GH,GQ,

由对称性可知$OM=OP=EN=DN=1$.
由正六边形的性质,得$ON=2\sqrt{3}$,
∴$OD=\sqrt{DN^{2}+ON^{2}}=\sqrt{13}=OF$.
∴$MF=\sqrt{13}-1$.
由正六边形的性质,知$△GFH,△GHQ,△GQM$都是正三角形,$∴FH=\frac{1}{2}MF=\frac{\sqrt{13}-1}{2}$.故选D.
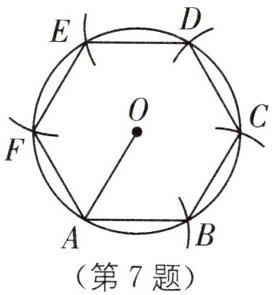
7. (2024·天津西青区期末)如图,已知点 $A$ 是半径为3的 $\odot O$ 上任意一点,以点 $A$ 为圆心、 $OA$ 为半径作弧,交 $\odot O$ 于点 $B$,以点 $B$ 为圆心, $OA$ 为半径作弧交 $\odot O$ 于点 $C$,同上述作图方法逆时针作出点 $D,E,F$,依次连接 $A→B→C→D→E→F→A$,则这个多边形的周长为______
18
.
答案:
18
查看更多完整答案,请扫码查看


