《2025年实验班提优训练九年级数学上册人教版》

1. (2025·广西期中)抛物线$y = - 2x^2 + 1$的对称轴是(B).
A. $x$轴
B. $y$轴
C. 直线$y = 0$
D. 直线$x = 1$

答案： B

2. (2025·江苏苏州姑苏区景范中学月考)将二次函数$y = x^2 + 1的图象沿y$轴向下平移2个单位长度,则得到的图象对应的函数解析式为(C).
A. $y = x^2 + 3$
B. $y = x^2 + 2$
C. $y = x^2 - 1$
D. $y = x^2 - 2$

答案： C

3. (2025·陕西西安期中)抛物线$y = 1 - 3x^2$的顶点是____(0,1).

答案： (0,1)

4. 实验班原创 已知二次函数$y = ax^2 + 2的图象经过点(1,1)$,则这个二次函数的解析式为y=−x²+2.

答案： y=−x²+2

5. 教材P33练习·变式(2025·福建厦门湖里区华师希平双语学校月考)在如图所示的平面直角坐标系中画出二次函数$y = \frac{1}{4}x^2 + 1与二次函数y = - \frac{1}{4}x^2 - 1$的图象,并说明两个函数图象性质的相同点与不同点.

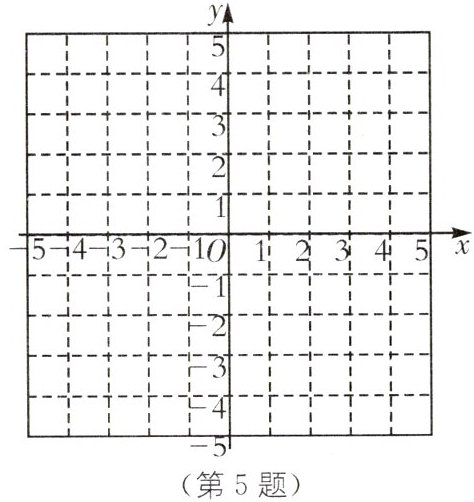
答案：
函数图象如图所示:
　　　　
相同点:①抛物线的开口的大小相同;②对称轴都是y轴;③顶点到x轴的距离相同.
不同点:①开口的方向不同;②当x＞0时，函数y=$\frac{1}{4}$x²+1随x的增大而增大，函数y=−$\frac{1}{4}$x²−1随x的增大而减小;当x＜0时,函数y=$\frac{1}{4}$x²+1随x的增大而减小,函数y=−$\frac{1}{4}$x²−1随x的增大而增大.
归纳总结　形如y=ax²+k的二次函数的图象的显著特征是对称轴为y轴，顶点在y轴上.

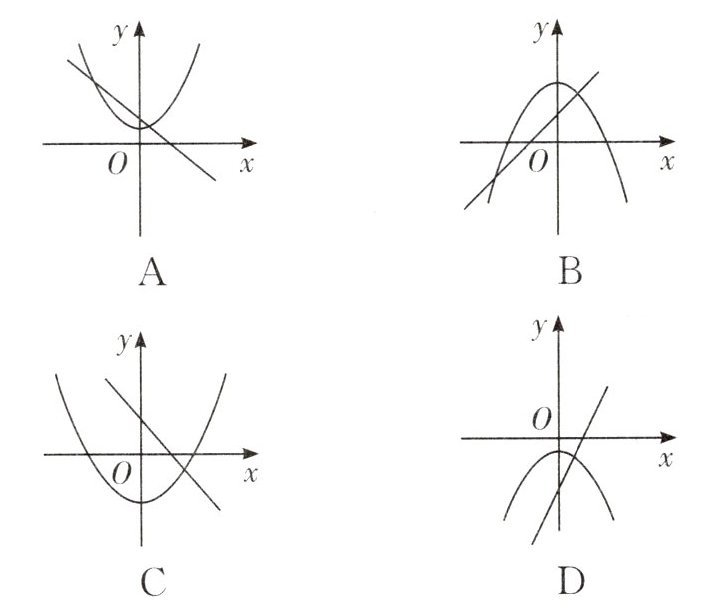
6. 在同一平面直角坐标系中,一次函数$y = ax + k与二次函数y = kx^2 + a$的图象可能是(C).

答案： C　[解析]A.由抛物线可知,a＞0,k＞0,由直线可知,a＜0,k＞0,矛盾,故本选项错误,不符合题意;
B.由抛物线可知,a＞0,k＜0,由直线可知,a＞0,k＞0,矛盾，故本选项错误，不符合题意;
C.由抛物线可知,a＜0,k＞0,由直线可知,a＜0,k＞0,故本选项正确，符合题意;
D.由抛物线可知,a＜0,k＜0,由直线可知,a＞0,k＜0,矛盾，故本选项错误，不符合题意.故选C.
思路引导　解决二次函数图象与其他函数图象相结合问题时，先根据给定的函数或函数图象判断出一个函数关系式中系数的符号，然后判断另一个函数关系式中系数的符号，对应符号相同的即为正确选项.

7. 如果将抛物线$y = x^2 - 1$绕着原点旋转180°得到一条新抛物线,那么下列关于这两条抛物线的描述中,正确的是(D).
A. 开口方向相同
B. 顶点坐标相同
C. 变化情况相同
D. 对称轴相同

答案： D　[解析]A.它们的开口方向相反,不符合题意;B.它们的顶点坐标关于原点对称，不符合题意;C.它们的开口方向相反，顶点坐标关于原点对称,即选项的变化情况不相同，不符合题意;D.它们的对称轴相同,符合题意.故选D.

8. (2024·赤峰中考)如图,正方形$ABCD的顶点A$,$C在抛物线y = - x^2 + 4$上,点$D在y$轴上.若$A$,$C两点的横坐标分别为m$,$n(m ＞ n ＞ 0)$,下列结论正确的是( ).

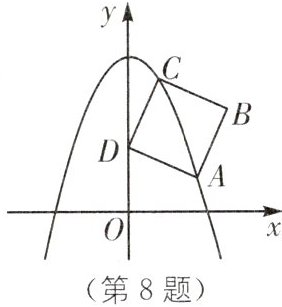
A. $m + n = 1$
B. $m - n = 1$
C. $m = 1$
D. $\frac{m}{n} = 1$

答案：
B　[解析]如图,分别过点A和点C作y轴的垂线，垂足分别为M和N,将A,C两点的横坐标代入函数解析式,得点A的坐标为(m,−m²+4),点C的坐标为(n,−n²+4),
∴AM=m,MO=−m²+4,CN=n,NO=−n²+4.
∵四边形ABCD是正方形，
∴AD=CD,∠ADC=90°,
∴∠CDN +∠ADM=∠ADM+∠DAM=90°,
∴∠CDN=∠DAM.
　　　　　　　　　　　　　　　
在△CDN和△DAM中,
$\begin{cases}\angle CND = \angle DMA = 90^{\circ}\\\angle CDN = \angle DAM\\CD = AD\end{cases}$
∴△CDN≌△DAM(AAS),
∴DM=CN=n,DN=AM=m,
∴MN=DM+DN=m+n.
∵MN=NO−MO=m²−n²,
∴m²−n²=m+n,即(m+n)(m−n)=m+n.
∵m＞n＞0,
∴m+n≠0,
∴m−n=1.故选B.

9. (四川南充高级中学自主招生)已知函数$y = - \frac{1}{2}x^2 + \frac{13}{2}$在$0 ＜ a \leq x \leq b$时,有$2a \leq y \leq 2b$,则$(a,b) = $(1,3).

答案： (1,3)　[解析]若0＜a≤x≤b,
则有$\begin{cases}2a = -\frac{1}{2}b^2 + \frac{13}{2}\\2b = -\frac{1}{2}a^2 + \frac{13}{2}\end{cases}$，解得$\begin{cases}a = 1\\b = 3\end{cases}$，即(a,b)=(1,3).