《2025年实验班提优训练九年级数学上册人教版》

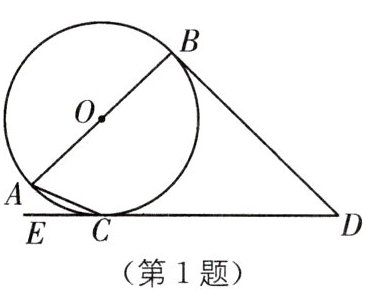
1. (2024·甘南州中考)如图,AB是$\odot O$的直径,DB,DE分别切$\odot O$于点B,C,若$∠ACE= 18^{\circ }$,则$∠D$的度数是(B).

A. $18^{\circ }$
B. $36^{\circ }$
C. $48^{\circ }$
D. $72^{\circ }$

答案： B

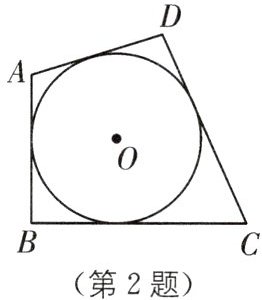
2. (2025·江苏泰州姜堰四中月考)如图,四边形ABCD是$\odot O$的外切四边形,且$AB= 8,CD= 12$,则四边形ABCD的周长为____40.

答案： 40

3. (2024·山东滨州滨城区期中)如图,$\odot O$内切于正方形ABCD,O为圆心,作$∠MON= 90^{\circ }$,其两边分别交BC,CD于点N,M,若$CM+CN= 10$,则$\odot O$的面积为____.

答案：
25π [解析]如图,设$\odot O$与正方形ABCD的边CD切于点E,与BC切于点F,连接OE,OF,则四边形OECF是正方形，
　　　　　　　　　　　　　　　　　
∴CF=CE=OE=OF,
∠OEM=∠OFN=∠EOF=90°.
∵∠MON=90°,
∴∠EOM=∠FON,
∴△OEM≌△OFN(ASA),
∴EM=NF,
∴CM+CN=CE+CF=10,
∴OE=5,
∴$\odot O$的面积为25π.

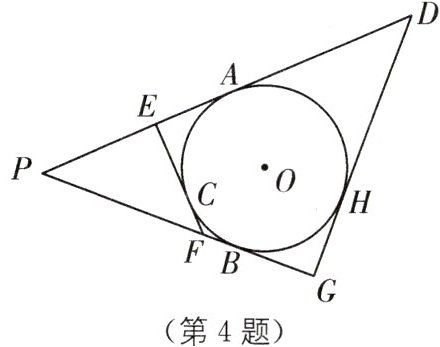
4. 教材P100例2·变式 如图,$\odot O是△GDP$的内切圆,切点分别为A,B,H,切线EF与$\odot O$相切于点C,分别交PA,PB于点E,F.
(1)若$△PEF$的周长为12,求线段PA的长;6
(2)若$∠G= 90^{\circ },GD= 3,GP= 4$,求$\odot O$的半径.1

答案：
(1)
∵$\odot O$是△GDP的内切圆，切点分别为点A,B,H,
∴PA=PB.
∵切线EF与$\odot O$相切于点C,
∴EA=EC,FB=FC.
∵△PEF的周长为12,
∴PE+EC+PF+FC=12,
∴PE+EA+PF+FB=12,即PA+PB=12,
∴PA=6.
(2)连接OB,OH,设$\odot O$的半径为r.
∵∠G=90°,GD=3,GP=4,
∴DP=$\sqrt{GD^{2}+GP^{2}}$=$\sqrt{3^{2}+4^{2}}$=5,
∴PA+DA=5.
∵$\odot O$是△GDP的内切圆,切点分别为点A,B,H,
∴OH⊥DG,OB⊥PG,PA=PB,DA=DH,GB=GH,
∴∠OBG=∠OHG=∠G=90°,
∴四边形OBGH是矩形.又OB=OH=r,
∴四边形OBGH是正方形，
∴GB=GH=r.
∵GP+GD=GB+PB+GH+DH=2r+PA+DA=2r+5,
∴2r+5=7,解得r=1,
∴$\odot O$的半径为1.

5. (2023·威海中考)在$△ABC$中,$BC= 3,AC= 4$,下列说法错误的是(C).
A. $1＜AB＜7$
B. $S_{△ABC}≤6$
C. $△ABC内切圆的半径r＜1$
D. 当$AB= \sqrt {7}$时,$△ABC$是直角三角形

答案： C [解析]A.由三角形三边关系,得4−3＜AB＜4+3,即1＜AB＜7,故A正确,不符合题意;B.当BC⊥AC时,$S_{△ABC}$最大,此时$S_{△ABC}=\frac{1}{2}×3×4=6$,故B正确,不符合题意;C.三角形内切圆半径r=$\frac{2S}{C}$,由$S_{△ABC}$最大为6,则此时r=$\frac{2×6}{3+4+5}=1$,所以r＜1错误,故C错误,符合题意;D.当AB=$\sqrt{7}$时,$BC^{2}=AC^{2}-AB^{2}$,所以△ABC是直角三角形，故D正确，不符合题意.故选C.

6. (浙江宁波慈溪中学保送生自主招生)如图,圆O的圆心在梯形ABCD的底边AB上,并与其他三边均相切,若$AB= 10,AD= 6$,则CB的长为( ).

A. 4
B. 5
C. 6
D. 无法确定

答案：
A [解析]设圆O的半径是R,圆O与AD,DC,CB相切于点E,F,H,连接OE,OD,OF,OC,OH,如图.设CD=y,CB=x,$S_{梯形ABCD}=S$,
　则$S=\frac{1}{2}(CD+AB)R=\frac{1}{2}(y+10)R$①,$S=S_{△BOC}+S_{△COD}+S_{△DOA}=\frac{1}{2}xR+\frac{1}{2}yR+\frac{1}{2}×6R$②,联立①②,得x=4,即CB=4.故选A.
　　　　　　　　　　　　　　
一题多解　连接OD,OC.
∵AD,CD是$\odot O$的切线，
∴∠ADO=∠ODC.
∵CD//AB,
∴∠ODC=∠AOD,
∴∠ADO=∠AOD,
∴AD=OA,
∵AD=6,
∴OA=6.
∵AB=10,
∴OB=4,同理可得OB=BC=4.故选A.

7. (2025·山东聊城四校联考期中)如图,点I为$△ABC$的内心,连接AI交$△ABC$的外接圆于点D,若$AI= 2CD$,点E为弦AC的中点,连接EI,IC,若$IC= 6,ID= 5$,则IE的长为____.

答案：
4 [解析]如图,延长ID到点M,使得DM=ID,连接CM;
∵I是△ABC的内心，
∴∠IAC=∠IAB,∠ICA=∠ICB.
∵∠DIC=∠IAC+∠ICA,∠DCI=
　∠BCD+∠ICB,∠BCD=∠IAB,
∴∠DIC=∠DCI,
　　　　　　　　　　　　　　　　　
∴DI=DC=DM,
∴∠ICM=90°.
　在Rt△ICM中,IM=2ID=10,IC=6,
∴CM=$\sqrt{IM^{2}-IC^{2}}$=8.
∵AI=2CD=10,
∴AI=IM.
∵AE=EC,
∴IE=$\frac{1}{2}$CM=4.

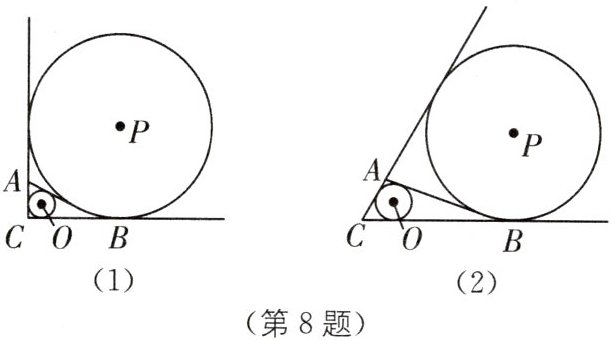
8. 在$△ABC$中,$∠C= α$,设$BC= a,AC= b,AB= c.\odot O是△ABC$的内切圆,$\odot P$分别与CA的延长线、CB的延长线以及直线AB均只有一个公共点,$\odot O$的半径为m,$\odot P$的半径为n.
(1)当$α=90^{\circ },b= 6,a= 8$时,$m= $____,$n= $____.
(2)如图(1),$α=90^{\circ }$,则$m= $____,$n= $____(用含有a,b,c的代数式表示);并求出$△ABC$的面积(用含有m,n的代数式表示).
(3)如图(2),$α=60^{\circ }$,求出$△ABC$的面积(用含有m,n的代数式表示).

答案：

(1)2　12 [解析]
∵α=90°,b=6,a=8,
∴c=10.如图
(1),设点D,E,F分别是$\odot P$的切点,连接PD,PE,PF,OA,OB,OC.
∵$S_{△BCA}=S_{△ABO}+S_{△ACO}+S_{△BCO}$,
∴$\frac{1}{2}×6×8=\frac{1}{2}×10m+\frac{1}{2}×6m+\frac{1}{2}×8m$,
∴m=2.
　由题意知,四边形DPEC为正方形,
∴n=PD=$\frac{1}{2}$(CD+CE).
　由切线长定理知,AF=AD,BF=BE,
∴n=$\frac{1}{2}$(CD+CE)=$\frac{1}{2}$(AD+AC+BE+BC)=$\frac{1}{2}$×(AB+AC+BC)=$\frac{1}{2}$×(10+6+8)=12.
　　　
(2)$\frac{ab}{a+b+c}$　$\frac{a+b+c}{2}$ [解析]如图
(1),由切线的性质可知PD⊥CD,PE⊥BC,PF⊥AB.
∵PD=PE=PF,设△ABC的面积为$S_{△ABC}$,周长为$C_{△ABC}$.同
(1),根据面积法可知m=$\frac{2S_{△ABC}}{C_{△ABC}}$=$\frac{2\times\frac{1}{2}ab}{a+b+c}$=$\frac{ab}{a+b+c}$.
∵n=$\frac{1}{2}$(CD+CE)=$\frac{1}{2}$(AD+AC+BE+BC)=$\frac{1}{2}$×(AB+AC+BC)=$\frac{1}{2}C_{△ABC}$=$\frac{a+b+c}{2}$,
∴$S_{△ABC}=\frac{mC_{△ABC}}{2}=mn$.
(3)如图
(2),连接CP.
　由切线长定理,得CD=CE=$\frac{1}{2}$(CD+CE)=$\frac{1}{2}$(AD+AC+BE+BC)=$\frac{1}{2}$(AB+AC+BC)=$\frac{1}{2}C_{△ABC}$.
∵PD⊥CD,PE⊥BC,
∴CP平分∠ACB,
∴∠PCE=30°,
∴n=PE=$\frac{CE}{\sqrt{3}}$=$\frac{C_{△ABC}}{2\sqrt{3}}$=$\frac{\sqrt{3}C_{△ABC}}{6}$.
∵m=$\frac{2S_{△ABC}}{C_{△ABC}}$,
∴$S_{△ABC}=\frac{mC_{△ABC}}{2}=\sqrt{3}mn$.