《2025年滚动迁移中考总复习数学山西专版》

考点二 全等三角形的应用
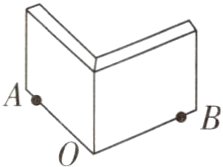
5. 原创 如图，某“综合与实践”小组准备测量墙角点O两侧点A和点B之间的距离，请完善以下测量过程.
任务：(1)画出测量示意图.（在原图上画）
(2)写出你设计的测量方案，并说明理由.

答案：
解:
(1)示意图如答图1所示.
(2)测量方案:延长AO至点C,延长BO至点D,通过测量使得OC = OA,OD = OB,量出CD的长就是点A和点B之间的距离.理由如下:如答图2,由测量方案可知 OA = OC,OB = OD,∠AOB = ∠COD,
∴△AOB≌△COD(SAS).
∴AB = CD.

核心素养提升—问题解决
太原双塔寺，因其寺内巍峨壮观、耸入云端的两座古塔而得名，是太原市的代表建筑之一. 设A，B两点分别为双塔寺中一座古塔底座的两端（A，B两点均在地面上）. 某学习小组想要测量A，B两点之间的距离，因为A，B两点间的实际距离无法直接测量，所以设计出了如下两种方案：
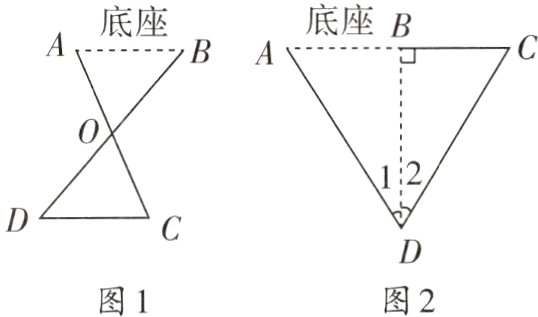
甲：如图1，在平地上取一个可以直接到达点A，B的点O，连接AO并延长到点C，连接BO并延长到点D，使$CO = AO$，$DO = BO$，连接DC，测出DC的长即可.
乙：如图2，先确定直线AB，过点B作$BD\perp AB$，在点D处用测角仪确定$\angle 1 = \angle 2$，射线DC交直线AB于点C，最后测出BC的长即可.
(1)请用所学知识论证甲、乙两种方案的合理性.
(2)如果让你参与测量，你会选择哪一种方案？请说明理由.

答案： 解:
(1)甲:在△ABO与△CDO中，$\begin{cases}AO = CO,\\\angle AOB = \angle COD,\\BO = DO,\end{cases}$
∴△ABO≌△CDO(SAS).
∴AB = CD.乙:
∵DB⊥AC,
∴∠ABD = ∠CBD = 90°.在△ABD与△CBD中，$\begin{cases}\angle ABD = \angle CBD,\\BD = BD,\\\angle 1 = \angle 2,\end{cases}$
∴△ABD≌△CBD(ASA).
∴AB = CB.
(2)选择甲方案，理由:甲方案操作简单，容易测量.