《2025年滚动迁移中考总复习数学山西专版》

(2024省适应性二)应县木塔，全称佛宫寺释迦塔，位于山西省朔州市应县西北佛宫寺内，是中国现存最高最古老的一座木构塔式建筑，与意大利比萨斜塔、巴黎埃菲尔铁塔并称“世界三大奇塔”。某校综合与实践小组测量应县木塔的高度，形成了如下不完整的实践报告：

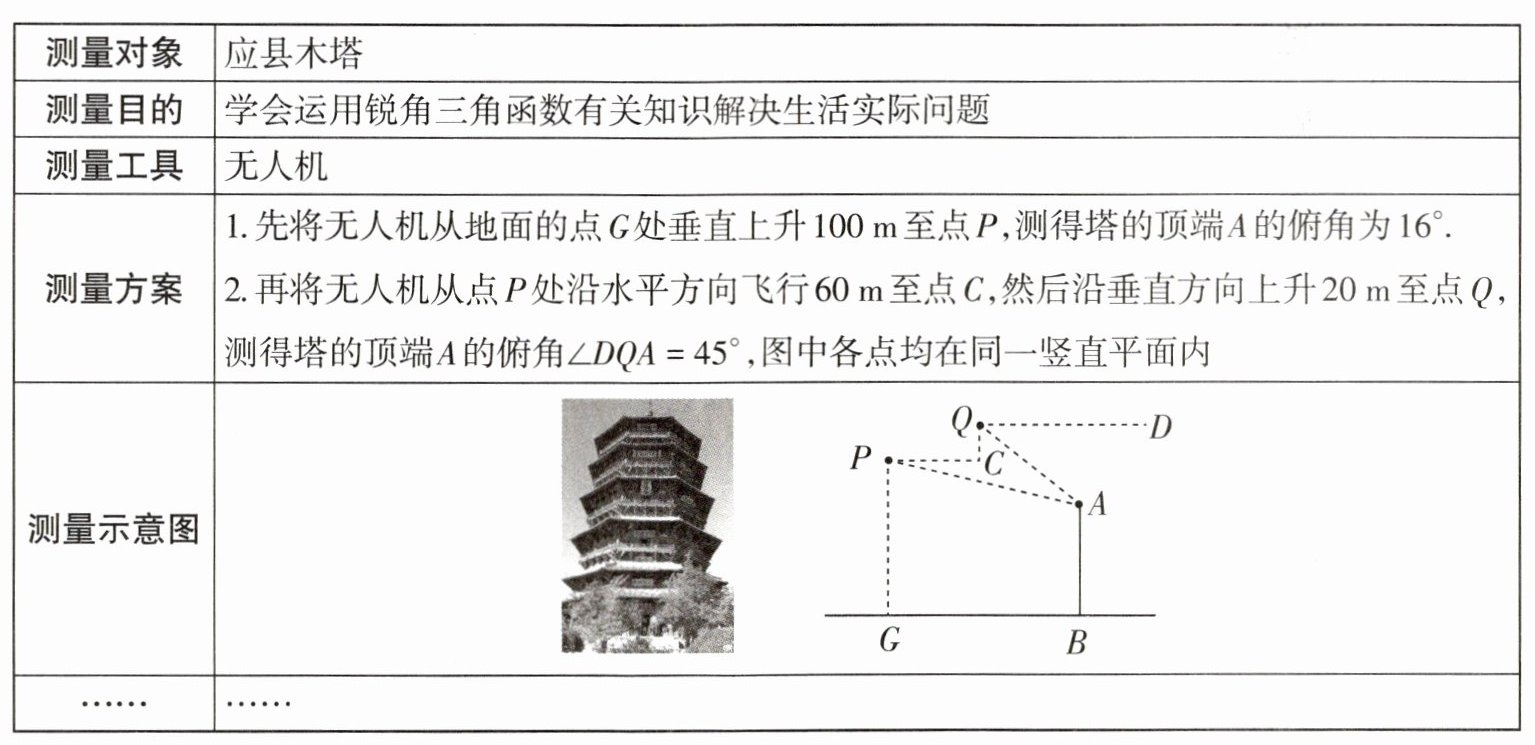
请根据以上测量数据，求应县木塔AB的高度。(结果精确到0.1 m，参考数据：sin 16° ≈ 0.28，cos 16° ≈ 0.96，tan 16° ≈ 0.29)

答案：
解:如答图，延长BA交QD于点F，延长PC交射线BA于点E,
　　　　　　　　　　
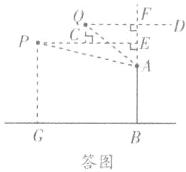
则四边形QCEF和四边形PGBE为矩形.
由题意得,PC=60,CQ=20,PG=100,
∴BE=PG=100,EF=CQ=20,QF=CE;
设AE为xm，则AF=AE+EF=x+20,
在Rt△AQF中,∠AFQ=90°,
∴tan∠AQF=$\frac{AF}{QF}$
∵∠AQD=45°,
∴tan45°=$\frac{AF}{QF}$=1,
即AF=QF=CE=x+20.
∴PE=PC+CE=60+x+20=x+80.
在Rt△PEA中,∠PEA=90°,
∴tan∠APE=$\frac{AE}{PE}$
∵∠APE=16°，
∴tan16°=$\frac{AE}{PE}$≈0.29,即AE=0.29PE.
∴x=0.29(x+80),解得x≈32.68.
∴AB=BE−AE=100−32.68=67.32≈67.3(m).
答:应县木塔的高度AB约为67.3m.