第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
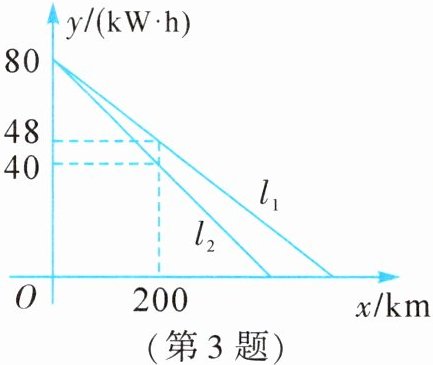
3. 某公司生产了 A,B 两款新能源电动汽车。如图,$ l_1 $,$ l_2 $ 分别表示 A 款、B 款新能源电动汽车充满电后电池的剩余电量 $ y $(kW·h)与行驶路程 $ x $(km)之间的关系。当这两款新能源电动汽车的行驶路程都是 300 km 时,A 款新能源电动汽车电池的剩余电量比 B 款新能源电动汽车电池的剩余电量多多少千瓦时?
]
]

答案:
A 款新能源电动汽车每千米的耗电量为$(80-48)÷200=0.16(kW\cdot h)$,B 款新能源电动汽车每千米的耗电量为$(80-40)÷200=0.2(kW\cdot h)$。所以$l_{1}$对应的函数表达式为$y_{1}=80-0.16x,l_{2}$对应的函数表达式为$y_{2}=80-0.2x$。当$x=300$时,$y_{1}=80-0.16×300=32,y_{2}=80-0.2×300=20,32-20=12(kW\cdot h)$。当这两款新能源电动汽车的行驶路程都是 300 km 时,A 款新能源电动汽车电池的剩余电量比 B 款新能源电动汽车电池的剩余电量多12 kW·h
4. 某科技研发中心有 50 名工作人员,其中技术员 20 名、操作员 30 名。现将这 50 名工作人员派往 A,B 两个公司去研发产品,两个公司的月工资情况如下。
| | 技术员工资/(万元/月) | 操作员工资/(万元/月) |
| ---- | ---- | ---- |
| A 公司 | 1.8 | 1.6 |
| B 公司 | 1.6 | 1.2 |
(1) 若派往 A 公司 $ x $ 名技术员,余下的工作人员全部派往 B 公司,求这 50 名工作人员的月工资总额 $ y $(万元)与技术员 $ x $(名)之间的关系式,并写出 $ x $ 的取值范围;
(2) 根据研发需要,50 名工作人员派往 A 公司 40 名,派往 B 公司 10 名,求月工资总额的最小值。
| | 技术员工资/(万元/月) | 操作员工资/(万元/月) |
| ---- | ---- | ---- |
| A 公司 | 1.8 | 1.6 |
| B 公司 | 1.6 | 1.2 |
(1) 若派往 A 公司 $ x $ 名技术员,余下的工作人员全部派往 B 公司,求这 50 名工作人员的月工资总额 $ y $(万元)与技术员 $ x $(名)之间的关系式,并写出 $ x $ 的取值范围;
(2) 根据研发需要,50 名工作人员派往 A 公司 40 名,派往 B 公司 10 名,求月工资总额的最小值。
答案:
(1)根据题意,派往 B 公司$(20-x)$名技术员和 30 名操作员,则$y=1.8x+1.6(20-x)+1.2×30=0.2x+68(0≤x≤20)$
(2)设派往 A 公司 m 名技术员,则派往 B 公司$(20-m)$名技术员,派往 A 公司$(40-m)$名操作员,派往 B 公司$(m-10)$名操作员。设月工资总额为 W 万元,则$W=1.8m+1.6(20-m)+1.6(40-m)+1.2(m-10)=-0.2m+84$。因为$-0.2<0$,所以 W 的值随着 m 值的增大而减小。因为$0≤m≤20$,所以当$m=20$时,W 的值最小,$W_{最小}=-0.2×20+84=80$,所以月工资总额的最小值为 80 万元
(1)根据题意,派往 B 公司$(20-x)$名技术员和 30 名操作员,则$y=1.8x+1.6(20-x)+1.2×30=0.2x+68(0≤x≤20)$
(2)设派往 A 公司 m 名技术员,则派往 B 公司$(20-m)$名技术员,派往 A 公司$(40-m)$名操作员,派往 B 公司$(m-10)$名操作员。设月工资总额为 W 万元,则$W=1.8m+1.6(20-m)+1.6(40-m)+1.2(m-10)=-0.2m+84$。因为$-0.2<0$,所以 W 的值随着 m 值的增大而减小。因为$0≤m≤20$,所以当$m=20$时,W 的值最小,$W_{最小}=-0.2×20+84=80$,所以月工资总额的最小值为 80 万元
查看更多完整答案,请扫码查看


