《2025年新课程同步学案八年级数学上册北师大版》

5. 一只兔子正在洞穴正南 $60\ m$ 的地方觅食,一只狼在兔子正东 $80\ m$ 处,此时兔子看到狼便急忙向自己的洞穴奔去,但狼以兔子速度的 $2$ 倍跑向兔子洞穴处进行拦截,你认为兔子能逃走吗? 请说明理由。

答案： 兔子不能逃走。理由如下:由题目可抽象出图形，如图,由勾股定理,得$AC^{2}=AB^{2}+BC^{2}=60^{2}+80^{2}=100^{2}$,所以$AC=100$ m。因为狼的速度是兔子速度的2倍,而$60×2＞100$,所以兔子不能逃走

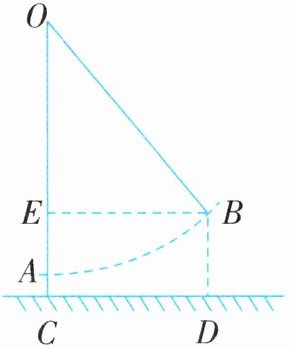
明朝数学家程大位在《算法统宗》中以《西江月》词牌叙述了一道“荡秋千”的问题:平地秋千未起,踏板一尺离地。送行二步与人齐,五尺人高曾记……翻译成现代文:如图,秋千 $OA$静止时,踏板离地高一尺($AC = 1$ 尺,“尺”是我国传统长度单位),将它往前推进两步($EB = 10$ 尺),此时踏板升高离地五尺($BD = 5$ 尺),求秋千绳索 $OB$ 的长度。

]

答案： 设$OA=OB=x$尺。因为$EC=BD=5$尺,$AC=1$尺,所以$EA=EC - AC=5 - 1=4$(尺),所以$OE=OA - AE=(x - 4)$尺。在$Rt\triangle OEB$中,$OE=(x - 4)$尺,$OB=x$尺,$EB=10$尺,根据勾股定理,得$x^{2}=(x - 4)^{2}+10^{2}$,解得$x=14.5$。即秋千绳索OB的长度是14.5尺

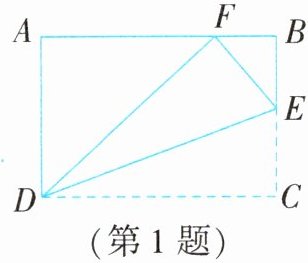
1. 如图,在长方形 $ABCD$ 中,$AB = 5$,$AD = 3$,点 $E$ 为 $BC$ 上一点,把$\triangle CDE$ 沿 $DE$ 翻折,点 $C$ 恰好落在 $AB$ 边上的点 $F$ 处,则 $CE$ 的长是(D)。

A.$1$
B.$\dfrac{4}{3}$
C.$\dfrac{3}{2}$
D.$\dfrac{5}{3}$

答案： D