《2025年新课程同步学案八年级数学上册北师大版》

4. 某市在市政改造中修建了一个圆形的街心花园，已知花园的面积为 $ 6280 \, m^{2} $，那么花园的半径约为(B)。($\pi$取 3.14)

A.32 m
B.45 m
C.68 m
D.48 m

答案： B

5. 估算：$\sqrt{135}$的整数部分是11；$-\sqrt[3]{200}$的整数部分是-5。

答案： 11 -5

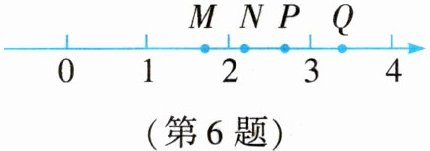
6. 如图，$ M $，$ N $，$ P $，$ Q $ 是数轴上的四个点，这四个点中最适合表示$\sqrt{7}$的点是P。

答案： P

7. 下列比较各组数的大小错误的是(C)。

A.$-2 ＜ -1$
B.$\pi ＜ \sqrt{17}$
C.$\frac{5}{2} ＞ \sqrt{10}$
D.$\frac{1}{3} ＞ 0.3$

答案： C

8. 一个正方体的体积为 $ 100 \, cm^{3} $，它的棱长 $ x $ 满足(A)。

A.$ 3 \, cm ＜ x ＜ 5 \, cm $
B.$ 5 \, cm ＜ x ＜ 7 \, cm $
C.$ 7 \, cm ＜ x ＜ 9 \, cm $
D.$ 9 \, cm ＜ x ＜ 10 \, cm $

答案： A

9. 将$\sqrt{5}$，$\pi$，0，-6 用“＜”连接起来，可表示为-6＜0＜√5＜π。

答案： -6＜0＜√5＜π

10. 通过估算，比较下列各组数的大小：
(1)$\sqrt{19}$＜4.5；(2)$-\sqrt{6}$＞-2.5；
(3)$\sqrt[3]{513}$＜8.1；(4)$\frac{\sqrt{7}-1}{2}$＜1；
(5)$2\sqrt{11}$＜$3\sqrt{5}$；(6)$\frac{\sqrt{6}-1}{3}$＜$\frac{1}{2}$。
利用估算可以比较两个无理数或有理数和无理数之间的大小，在比较时，我们一般采用分析的方法，将无理数取一个适合的近似值，再进行具体的比较。

答案：
(1)＜
(2)＞
(3)＜
(4)＜
(5)＜
(6)＜

11. 利用计算器比较下列各组数的大小：
(1)$\sqrt{18}$和$\sqrt[3]{75}$；(2)$\frac{\sqrt{2}-4}{3}$和$-\frac{17}{20}$。

答案：
(1)√18＞∛75
(2)(√2-4)/3＜-17/20

12. 利用计算器计算：
$\cdots$，$\sqrt{0.0625}$，$\sqrt{0.625}$，$\sqrt{6.25}$，$\sqrt{62.5}$，$\sqrt{625}$，$\sqrt{6250}$，$\sqrt{62500}$，$\cdots$。
计算后，分析结果，你发现了什么规律？

答案： 用计算器计算所得结果如下:…,0.25,0.7906,2.5,7.906,25,79.06,250,…。分析计算结果可以发现:被开方数的小数点每向右(左)移动两位,算术平方根的小数点相应地向右(左)移动一位(答案合理即可)