第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
6. 勾股定理a² + b² = c²本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫作勾股数组。毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:(3,4,5),(5,12,13),(7,24,25),…。观察上面的勾股数组可以发现:4 = 1×(3 + 1),12 = 2×(5 + 1),24 = 3×(7 + 1),…。分析上面的规律,则第5个勾股数组为
(11,60,61)
。
答案:
6. (11,60,61)
7. 将勾股数3,4,5分别扩大到原来的2倍、3倍、4倍……可以得到勾股数6,8,10;9,12,15;12,16,20;…。我们把3,4,5这样的勾股数称为基本勾股数,请写出两组不同于以上所给出的基本勾股数:
5,12,13;7,24,25(答案不唯一)
。
答案:
7.5,12,13;7,24,25(答案不唯一)
1. 如图,在由边长为1的正方形组成的网格图中,有a,b,c,d四条线段,下列能构成一个直角三角形三边的线段是(
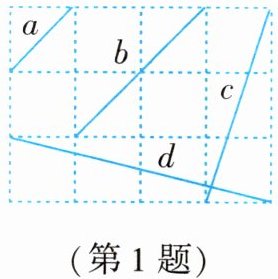
A.a,b,c
B.b,c,d
C.a,b,d
D.a,c,d
]
A
)。
A.a,b,c
B.b,c,d
C.a,b,d
D.a,c,d
]
答案:
1. A
2. 张老师在一次“探究性学习”的课程中,设计了如下数表。
|n|2|3|4|5|…|
|----|----|----|----|----|----|
|a|2² - 1|3² - 1|4² - 1|5² - 1|…|
|b|4|6|8|10|…|
|c|2² + 1|3² + 1|4² + 1|5² + 1|…|
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n > 1)的代数式表示:a =
(2)以a,b,c为边长的三角形是不是直角三角形?为什么?
|n|2|3|4|5|…|
|----|----|----|----|----|----|
|a|2² - 1|3² - 1|4² - 1|5² - 1|…|
|b|4|6|8|10|…|
|c|2² + 1|3² + 1|4² + 1|5² + 1|…|
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n > 1)的代数式表示:a =
n² - 1
,b = 2n
,c = n² + 1
。(2)以a,b,c为边长的三角形是不是直角三角形?为什么?
答案:
2.
(1)$n^{2}-1$ $2n$ $n^{2}+1$
(2)是直角三角形。理由如下:因为$a^{2}+b^{2}=(n^{2}-1)^{2}+(2n)^{2}=n^{4}+2n^{2}+1$,$c^{2}=(n^{2}+1)^{2}=n^{4}+2n^{2}+1$,所以$a^{2}+b^{2}=c^{2}$,所以以a,b,c为边长的三角形是直角三角形
(1)$n^{2}-1$ $2n$ $n^{2}+1$
(2)是直角三角形。理由如下:因为$a^{2}+b^{2}=(n^{2}-1)^{2}+(2n)^{2}=n^{4}+2n^{2}+1$,$c^{2}=(n^{2}+1)^{2}=n^{4}+2n^{2}+1$,所以$a^{2}+b^{2}=c^{2}$,所以以a,b,c为边长的三角形是直角三角形
查看更多完整答案,请扫码查看


